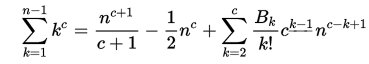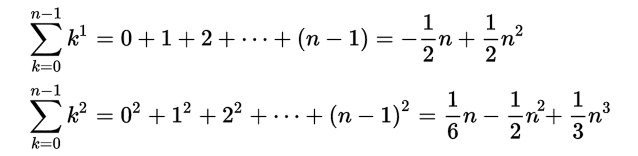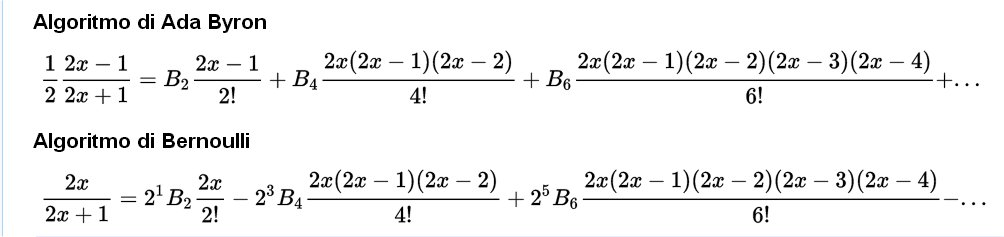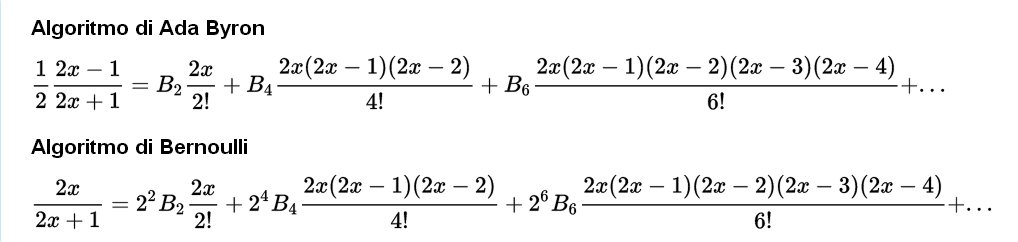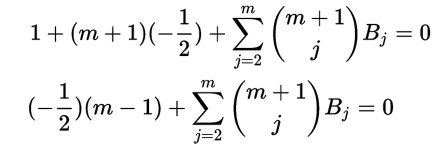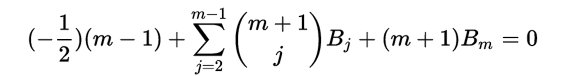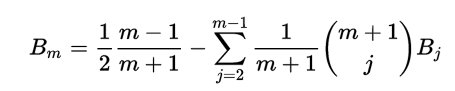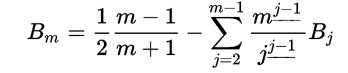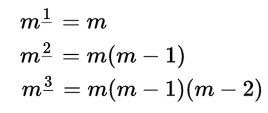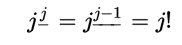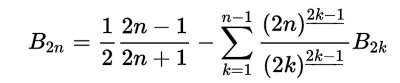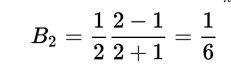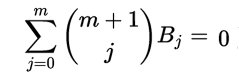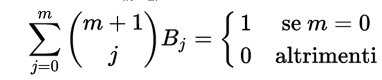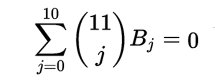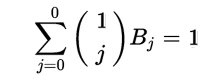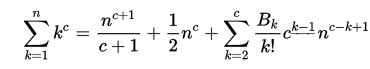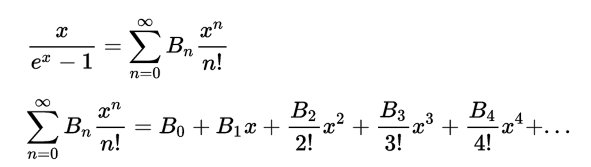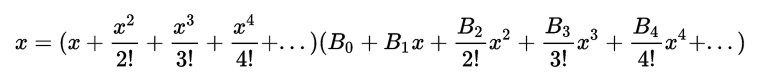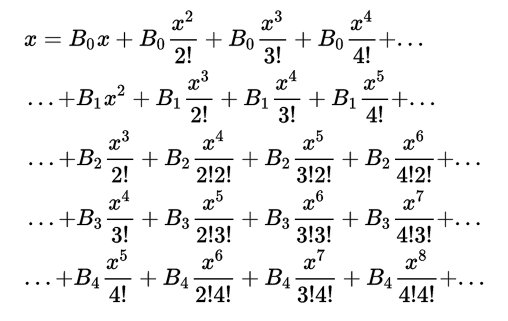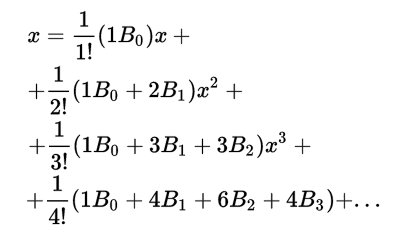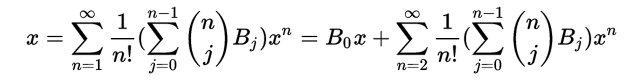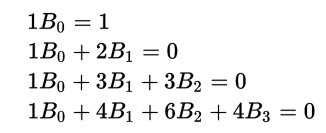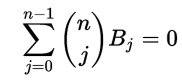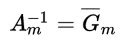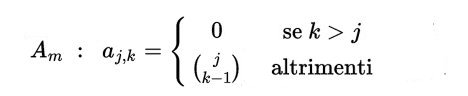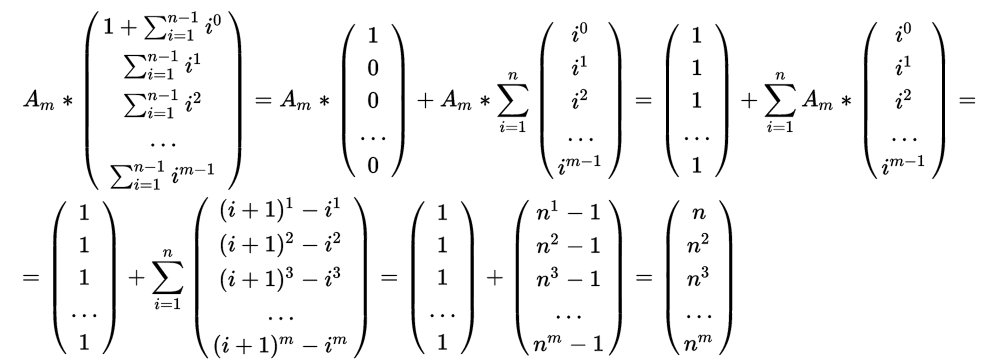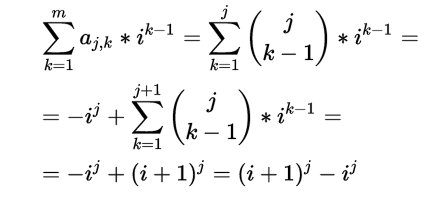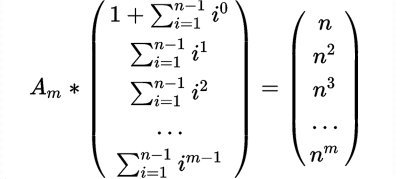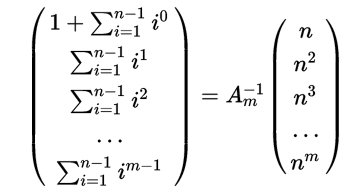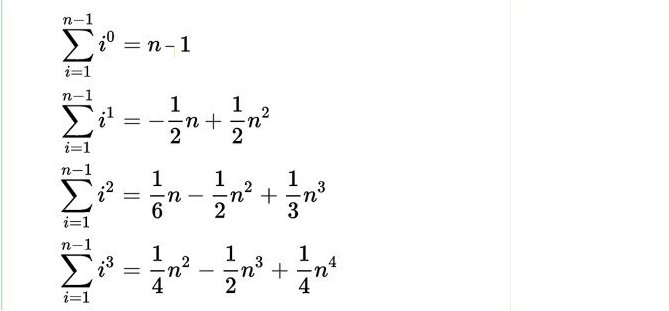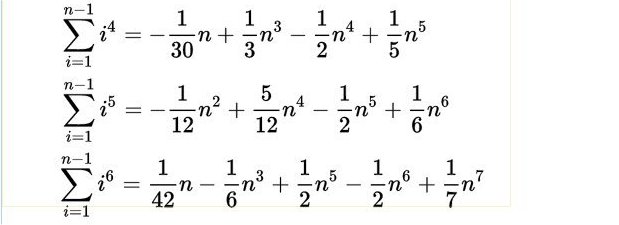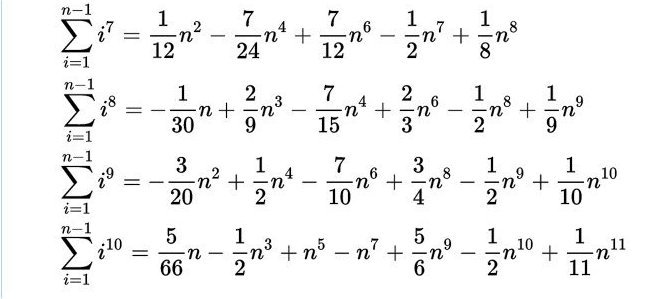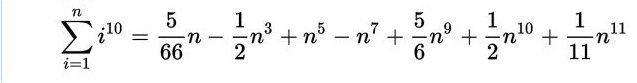Internet e l’algoritmo di Ada Byron,
contessa di Lovelace e incantatrice di numeri
di Giorgio Pietrocola
giorgio.pietrocola[at]gmail.com
30 Giugno 2017
Indice
- Ada e il suo algoritmo
- Identificazione della formula
- Dimostrazione per via matriciale.
- Considerazioni sui miei studi
- Dimostrazione per via analitica
- La via matriciale, il teorema 1B
- Bibliografia
1. Ada e il suo algoritmo
La piccola Ada nacque a Londra nel 1815 da Anne Isabella Milbanke appassionata di matematica e dal famoso poeta romantico Lord Byron che però non conobbe mai perché abbandonò per sempre la famiglia alla sua nascita. La piccola avviata dalla madre allo studio della matematica dimostrò subito interesse e capacità. Fu seguita e apprezzata da ottimi matematici come Mary Sommerville, Augustus De Morgan e Charles Babbage. Nel 1842 Babbage tenne un seminario presso l’università di Torino, e Luigi Menabrea, giovane ingegnere italiano, pubblicò per la Bibliotèque Universelle di Ginevra “Notions sur la machine analytique de Charles Babbage”. Della traduzione inglese del testo Babbage incaricò la matematica da tempo sua collaboratrice, Ada Lovelace, che intanto si era sposata a vent’anni e aveva assunto il cognome del marito dal quale ebbe anche tre figli e il titolo di contessa di Lovelace.
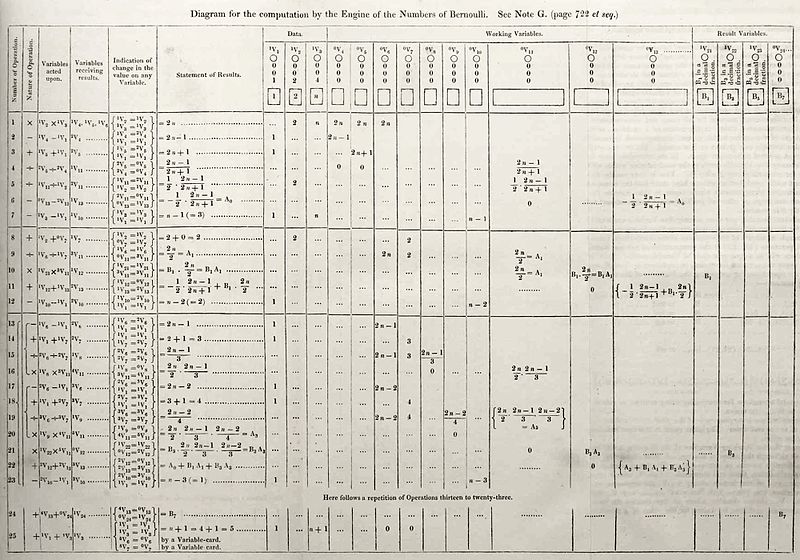
|
Fig.1 Diagramma della Nota G [5][1] di Ada Lovelace. Algoritmo per il calcolo dei numeri di Bernoulli in un programma pensato per la macchina analitica di Charles Babbage, un primo computer basato sulla meccanica che per i suoi alti costi non fu mai realizzato. (Cliccare qui per il diagramma ingrandito). |
Ada, l’incantatrice dei numeri, come amava definirla Charles arricchì il testo con le sue note che alla fine furono più ponderose del saggio che aveva tradotto. Ecco il diagramma della sua famosa nota G in cui, per la prima volta nella storia, con più di un secolo di anticipo, viene pubblicato un programma per elaboratore. Oggi tutti sanno cosa siano i computer e i loro programmi ma allora solo menti eccezionali e visionarie potevano immaginare qualcosa di simile. Il programma descritto in fig.1 ha lo scopo di calcolare i famosi numeri di Bernoulli che hanno preso il nome da Jacob Bernoulli il matematico svizzero che li fece conoscere al mondo nel 1713 quando fu pubblicato postumo il suo trattato “Ars conjectandi” in cui, pur senza poterne dare dimostrazione, presentava una mirabile regola
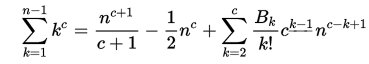
|
che permetteva di costruire, mediante particolari numeri, il polinomio per il calcolo delle somme di potenze di interi successivi per qualsiasi esponente intero positivo. Ecco i coefficienti dei primi polinomi riassunti qui sotto nella matrice di fig.2

|
Fig.2 Nella prima colonna ci sono i coefficienti dei monomi di primo grado dei polinomi calcolanti le somme di potenze. Sono quelli che oggi chiamiamo numeri di Bernoulli e indichiamo con B0 B1 B2 B3 B4 B5 B6 B7 B8 B9 B10... anche se Jacob, come anche Ada nel suo programma, cominciavano la sequenza ignorando i primi due e iniziando da quello che ai nostri tempi si indica con B2. Ada come si può vedere in fig.1 indica con B1 B3 B5... i numeri di Bernoulli dato che l’algoritmo usato calcola soltanto i numeri diversi da zero. Nella notazione attuale questi corrispondono a B2 B4 B6 etc.
Dalle righe si possono agevolmente ricostruire i polinomi. Per quanto riguarda la prima riga i conti piuttosto banali tornano ponendo 00 =1 Invece, dalla seconda e dalla terza riga otteniamo:
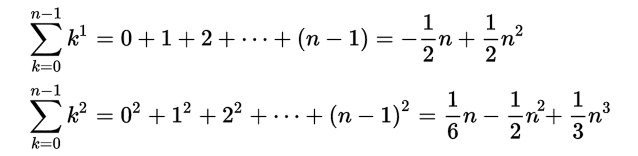 |
Come è noto il programma non potè essere provato da Ada perché per motivi economici quella straordinaria macchina che avrebbe anticipato l’era informatica di un secolo non potè essere costruita. Oggi possiamo giovarci della fase del “debug” per correggere quello che non funziona in un programma per computer ma per quel primo programma questo non fu possibile. Tuttavia guardando il diagramma riportato in fig.1 si può capire quale formula sia stata applicata per il calcolo automatico dei numeri di Bernoulli.
Ho deciso di scrivere su questo argomento perché nelle mie ricerche in rete, particolarmente nei siti in lingua italiana, ho trovato una moltitudine di errori, sempre gli stessi in diversi siti e perfino in una tesi. Questi errori, anche grossolani, come vedremo hanno potuto replicarsi indisturbati in un arco di tempo di 12 anni e si ritrovano ancora in molti siti che parlano di questo personaggio storico emblematico e del suo primo programma. Ho cercato di ricostruire, per quanto mi è stato possibile, gli avvenimenti. E’ una storia che credo possa essere utile a chi deve perfezionare quel senso critico indispensabile per giovarsi delle fonti disponibili in rete. La fonte più antica di quegli errori a cui ho potuto risalire è Wikipedia, la nota enciclopedia digitale su cui tutti possiamo scrivere, aggiungere e cancellare, Perfino in forma completamente anonima, identificati soltanto dai quattro byte di connessione. Nell’aprile 2005 un utente registrato come “Blanka”[2] crea una nuova pagina dal titolo “Algoritmo di Ada Lovelace per i numeri di Bernoulli” ecco la pagina del 2005 accessibile dalla cronologia presente in tutte le voci di questa mirabile opera collettiva. Dai registri di wikipedia risulta che i contributi di questo utente si sono limitati a questa voce e a un arco di tempo di pochi giorni. La pagina creata era, e così rimase per più di 12 anni, priva di validi riferimenti bibliografici. Non solo mancava la bibliografia ma era anche priva di note che rimandassero ad una fonte in rete, più o meno autorevole. Di norma in Wikipedia questa carenza viene presto segnalata dai frequentatori attivi, o wikipediani, e, se nessuno vi pone rimedio, la pagina, dopo non molto, viene proposta per la cancellazione. Oltre alla necessità di valutare le fonti, che condivide con le altre discipline, la matematica spesso offre la possibilità di verificare direttamente le formule proposte. Qui era possibile e anche abbastanza facile dato che si dovevano moltiplicare e sommare pochi termini ma nessuno per molto tempo si è curato di farlo. Oltre a identificare le formule che non funzionano non dovrebbe essere difficile, anche per un discreto studente di scuola media superiore, identificare altri grossolani errori presenti in molti passaggi.
In un primo momento gli errori mi erano sembrati semplici sviste e avevo creduto che dopo averli corretti il testo potesse andare ma ben presto mi sono accorto che quegli errori erano funzionali a ciò che si intendeva dimostrare.
Ma c’è qualcosa che per me è stato ancora più sorprendente della moltitudine di omissioni e di errori trovati in quel testo. Nonostante tutto ciò portasse discredito alla voce, ho provato a dar fiducia e ho cercato di correggere gli algoritmi che non funzionavano. Ecco come si presentavano:
Leggendo la nota G della stessa Lovelace come anche altre pubblicazioni in lingua inglese [6,3,4,5] presenti in rete risultava evidente che la prima formula pur essendo sbagliata poteva facilmente essere corretta e quindi aveva un corrispondente funzionante che ho individuato e ben verificato. Per la seconda formula, quella attribuita a Bernoulli, invece, non ero riuscito a trovare nulla di simile e sospettavo che fosse del tutto inventata. Nonostante fosse azzardato dare fiducia ad una formula che non trovava riscontri nei tanti testi consultati ed era contornata da moltitudini di errori, ho voluto supporre che esistesse qualcosa di simile e mi sono messo alla sua ricerca empirica.
Armato di foglio di calcolo, dopo svariati tentativi, rigorosi collaudi e una certa dose di immaginazione, grande è stata la mia sorpresa nello scoprire che una formula simile esisteva effettivamente.
Ecco le precedenti formule dopo le mie correzioni:
(con x numero intero positivo)
Quel Blanka che nel 2005 inserì quelle formule errate era un burlone sapiente oppure un ignorante in buona fede che ha copiato sbagliando da qualche altra ignota fonte magari già di seconda mano? Certo due formule sbagliate tanto simili a quelle giuste non si inventano facilmente dal nulla. Nel corso delle mie ricerche sui numeri di Bernoulli leggendo la Wikipedia in lingua inglese[3] mi era capitato un paragrafo quasi sicuramente aggiunto per gioco che avevo cancellato. Era stato intitolato provocatoriamente “debole funzione generatrice” ma nessuno ci aveva fatto caso finché, accorgendomi dell’inganno, ho cancellato tutto commentando che a mio modesto parere quella funzione era un po’ troppo debole.
Avendo trovato, ben nascosta, quella sconosciuta formula funzionante, ho provato, senza successo, a dare credito anche alla questione del confronto di algoritmi che a me sembrava e sembra tuttora ingiustificata.
Nella sua nota G Ada dichiara di aver preso in considerazione algoritmi alternativi che descrive con le relative formule ma tra questi non c’è la formula attribuita a Bernoulli. Nulla quindi
che giustifichi il particolare confronto tra il suo algoritmo e l’altro.
La nota G prosegue mostrando come la formula scelta derivi direttamente dalla funzione generatrice. Nelle mie ricerche ho riscontrato una certa difficoltà da parte di chi presenta questa formula servita per il primo programma della storia. Tale difficoltà nasce, a mio avviso, dal fatto che questa formula sembra introvabile nei documenti che oggi parlano dei numeri di Bernoulli e la si trova unicamente associata all’impresa della prima programmatrice. Insomma in molti autori sembra esserci la preoccupazione di giustificare adeguatamente una formula che da allora non si sa bene che fine abbia fatto.

|
Fig.3 Immagine tratta da “Charles Babbage Ada Lovelace and the Bernoulli number” di Thomas j.Misa University of Minnesota [4]. In questo documento disponibile in rete si vede lo sviluppo in serie della funzione generatrice. Viene usata la notazione usata da Ada e la formula da lei effettivamente applicata. Sul modo per derivare questa da quella si dà solo un vago cenno. |
Ma torniamo a raccontare lo sviluppo degli avvenimenti. Nonostante le evidenti carenze quella pagina proposta nel 2005 viene implicitamente accettata dalla comunità dei wikipediani e resiste con modifiche minime per molti anni.
Nel 2011 una studentessa si laurea in un’università italiana con una tesi su “Numeri di Bernoulli e loro applicazioni” e la tesi è pubblicata on line. Il terzo paragrafo tratta “L’algoritmo di Ada Lovelace per i numeri di Bernoulli” e riporta tale e quale il testo infondato e pieno di errori tratto dalla Wikipedia in lingua italiana che viene anche correttamente citata come fonte. Quando nel corso della mia ricerca sui numeri di Bernoulli, i primi di giugno del 2017, lessi su Wikipedia la pagina “Algoritmo di Ada Lovelace per i numeri di Bernoulli” questa si presentava così. Preso atto degli errori già descritti andai a cercare in rete una fonte non citata da cui potesse essere stata tratta quella pagina “martoriata”. Fu allora che mi imbattei in quella tesi di laurea. Non avendo ancora realizzato che la pagina enciclopedica era anteriore a quella fonte, scrissi al relatore della tesi segnalando gli errori riscontrati. Mi fu gentilmente risposto ringraziandomi ma aggiungendo di non poter esaminare la cosa in tempi brevi. Questo mi fece sospettare che Wikipedia non avesse usato quella fonte ma piuttosto fosse accaduto il contrario. Cercai conferma e la trovai sia nella cronologia di Wikipedia sia nella tesi stessa che, come detto, citava esplicitamente wikipedia.
Mi accorsi successivamente anche di altri siti in lingua italiana che avevano adottato, tali e quali, quelle formule e quel testo:
Decisi allora di pubblicare qualcosa su Internet per tentare di contrastare tanta dilagante disinformazione sull’argomento.
Visto che le spiegazioni in rete si erano rivelate insoddisfacenti, mi sono applicato autonomamente per cercare di capire la natura di quella formula misteriosa che Ada aveva scelto per il suo programma. Sono così arrivato a risolvere la questione e a dimostrare la cosa sia per via analitica, partendo dalla funzione generatrice, come indicano le fonti consultabili sia per una via alternativa, più breve, come immediato corollario del teorema “1B” sulle matrici inverse che dimostrai e pubblicai nel 2008 per Maecla [2]. Ho scoperto quindi finalmente quello che le fonti consultate non dicevano. La formula usata da Ada non è altro, come ci si sarebbe dovuto aspettare, che quella ricorsiva più semplice indicata da tutti i testi che si occupano dei numeri di Bernoulli.
2. Identificazione della formula usata
Questa formula è presente comunemente nei testi che trattano i numeri di Bernoulli perché permette di ricavarli agevolmente in modo ricorsivo. Cioè di trovare il successivo conoscendo tutti i precedenti. Eppure, anche se non sembra, come mostrerò, questa è anche la formula usata da Ada per il suo primo programma.
Perché allora la formula di Ada che si vede in basso nella fig.3 oggi sembra così difficile da riconoscere? perché non sembra presente nei trattati sui numeri di Bernoulli?
Il motivo è assai semplice, quella formula va riportata al contesto storico in cui fu utilizzata. Ada Lovelace viveva in un tempo in cui ancora non si consideravano B0=1 e B1=-½ , quelli che per i matematici odierni sono i primi due numeri di Bernoulli a dispetto del fatto che fu Jacob stesso il primo a non prenderli in considerazione nel suo famoso trattato. Questa differenza di notazioni ha come conseguenza che le formule di allora siano state riformulate con la nuova notazione e che non sia facilissimo riconoscerle. Per questo, come mostrerò, le nostre formule possono apparire assai diverse pur essendo nella sostanza equivalenti. Per trovare le loro formule dobbiamo sostituire nelle nostre i valori numerici dei primi due numeri della sequenza. Così facendo, in quella in questione, otteniamo:
da cui evidenziando l’ultimo termine:
e quindi esplicitando:
che equivale a:
Ecco dunque l’equazione di Ada espressa in notazione moderna. Nella formula abbiamo usato la notazione per il fattoriale discendente di cui ricordiamo il significato con degli esempi:
Ricordando anche che:
si ottiene così la formula effettivamente usata dalla Lovelace che giustamente trascura i valori che avrebbero portato ad un calcolo inutile dato che come è noto questi numeri sono alternativamente uguali a zero:
formula da usare per n>1 mentre per n=1 non c’è sommatoria da sottrarre e risulta semplicemente:
Scoperto tutto ciò l’ 11 giugno 2017, vista l’impossibilità di sanare i molteplici errori e non avendo trovato neppure una convincente giustificazione del confronto di algoritmi proposto ho inviato un mio agente segreto “79.35.70.171” con la missione di cancellare quella vecchia voce per proporne una del tutto nuova. Eccola subito dopo il drastico intervento a cui finora nessuno ha ritenuto opportuno opporsi (qui). Terminata questa operazione rispondo al professore relatore della tesi on line comunicandogli che se e quando avrà tempo per discutere con me dell’argomento potrà basarsi anche sull’attuale pagina di Wikipedia in lingua italiana.
3. Dimostrazione per via matriciale
Torniamo alla questione della dimostrazione della formula da cui abbiamo mostrato discendere quella di Ada. Dimostreremo non solo che per m>0:
ma, meglio ancora che per m=0,1,2,...,m risulta:
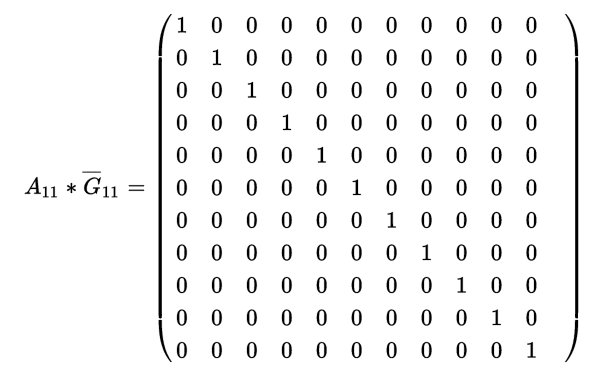
I coefficienti binomiali moltiplicanti Bj sono gli elementi della riga (m+1) del triangolo di tartaglia privati dell’ “1” finale, eccoli in una matrice di ordine 11:
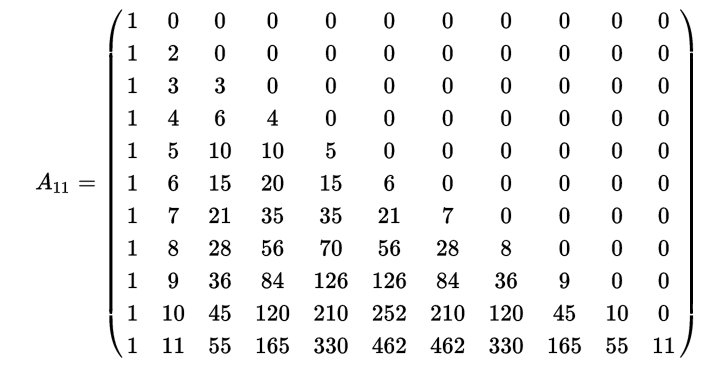
|
fig.4 “La matrice sfregiata” dà un triangolo di Tartaglia mutilato dell’ultimo elemento di ogni riga |
Nel teorema “1B” la cui dimostrazione rimandiamo all’ultimo paragrafo, ho dimostrato che, per ogni indice intero positivo, questa matrice è l’inversa di quella con i coefficienti dei polinomi per il calcolo delle somme di potenze di interi successivi. In particolare nel caso dell’indice 11 la matrice in fig.2 è l’inversa di A11 per cui abbiamo che il loro prodotto dà l’elemento neutro:
dunque in particolare moltiplicando l’ultima riga del “Tartaglia sfregiato” per la prima colonna dei numeri di Bernoulli:
e invece moltiplicando la prima riga per la prima colonna:
sono casi particolari facilmente generalizzabili che dovrebbero chiarire il mistero di queste formule di ricorrenza per i numeri di Bernoulli usate, come abbiamo mostrato, anche da Ada.
4. Considerazioni sui miei studi sui numeri di Bernoulli
Sono passati nove anni da quando ho pubblicato su Maecla il racconto delle mie scoperte sui numeri di Bernoulli e i relativi teoremi. Non so ancora se si tratti di una scoperta o di una riscoperta ma certamente dopo molte ricerche su internet credo di poter dire che se la mia è una via conosciuta non è molto frequentata. In questi anni non mi sono più occupato del problema ma ora mi sono nuovamente appassionato all’argomento e ho iniziato nuove ricerche ancora in corso. Sto cercando di sviluppare tutte le conseguenze del mio particolare approccio ai numeri di Bernoulli basato sulle matrici invece che sull’analisi matematica che costituisce una via certamente molto più praticata. Partendo dai miei teoremi sulle matrici inverse ho potuto dimostrare agevolmente molte proprietà di questi numeri come il loro annullarsi alternato. Ho anche potuto dimostrare la mirabile formula che Jacob Bernoulli aveva trovato e diffuso con il suo trattato postumo:
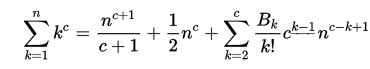
|
Questa formula esprime i coefficienti del generico polinomio per il calcolo della somma di potenze di interi successivi. Jacob l’aveva scoperta ma la dimostrazione fu data molto tempo dopo, nel 1834 da Carl Gustav Jacobi seguendo, a quanto sembra, la via analitica per la quale necessitano nozioni avanzate piuttosto problematiche come lo sviluppo di funzioni in serie infinite con i loro raggi di convergenza, la funzione zeta di Riemann etc. L’approccio con le matrici invece richiede solo la normale conoscenza dei coefficienti binomiali, dell’algebra e del calcolo matriciale e mi sembra molto più adatto a un livello di preparazione matematica da scuola media superiore. Insomma la mia ricerca si prefigge lo scopo di mostrare la percorribilità della “mia” via dato che, a quanto ho potuto constatare, oggi si percorre esclusivamente l’altra [3,4][4].
5. Dimostrazione per via analitica
La via analitica, alternativa a quella che propongo, parte dalla funzione generatrice con cui definisce l’infinita sequenza numerica bernoulliana e da questa ricava le sue proprietà. Per dimostrare quel che ho appena mostrato partendo dalle matrici si deve considerare:
poi sapendo che
si sostituisce, direi con disinvoltura, questo sviluppo in serie infinita nella funzione generatrice. Si procede quindi estendendo le regole ordinarie ai polinomi infiniti ottenendo:
e quindi distribuendo:
Infine sommando i monomi simili ordinati per grado che potete osservare sopra rappresentati lungo le linee diagonali si ha:
e, in forma compatta:
Dunque perché il polinomio dato dalla serie infinita nel secondo membro dell’uguaglianza sia uguale al monomio di primo grado a primo membro deve essere:
e quindi in generale per n>1
come dovevamo dimostrare
6. La via matriciale: il teorema 1B
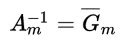
|
Si dimostra, per qualsiasi m, che i coefficienti dei polinomi per il calcolo della somma di n-1 potenze di interi successivi si possono ottenere invertendo una matrice triangolare ricavabile dal triangolo di Tartaglia eliminando l’ultimo elemento di ogni riga. |
Prendiamo in considerazione una matrice quadrata, di m righe e m colonne così definita:
Questa risulta essere una matrice triangolare in cui compare il triangolo di Tartaglia privato dell’ultimo elemento di ogni riga. La sua diagonale principale é formata dalla successione degli interi positivi il cui prodotto (m!) ne dà il determinante. (Per il caso particolare m=11 vedi fig.4)
Si ha
Nei primi due passaggi si è applicata la proprietà distributiva. Nel terzo,quando si è moltiplicata la matrice Am per il vettore di potenze si ottiene:
Dunque si è dimostrato che:
Moltiplicando i due membri a sinistra per l'inversa di Am otteniamo:
che fornisce la nota variante ai famosi polinomi per il calcolo delle somme di potenze di interi successivi.
Esempio con m=11:
O in forma equivalente:
__________
Per finire solo un accenno alle somme estese a n addendi. Per ottenerle basta aggiungere ai due membri n elevato alla potenza sommata. Si ottiene così un polinomio differente solo per un coefficiente che cambia segno.Per esempio nell’ultimo polinomio con n10 si ottiene:
Si dimostra in modo assai simile a quello visto che nel caso di somme con n addendi l’inversa della matrice dei coefficienti, rispetto al caso esaminato, cambia solo per l’alternanza dei segni.
7. Bibliografia e varia documentazione in rete
- Jacob Bernoulli, “Summa potestatis“ in “Artis Conjectandi”, p.97, 1713, digitalizzato su Internet Archive
- Giorgio Pietrocola, “Esplorando un antico sentiero:teoremi sulla somma di potenze di interi successivi”, 2008, Maecla
- Aditi Kar, “Lady Ada Lovelace and the analitycal engine”
- Thomas J. Misa,“Charles Babbage Ada Lovelace and the Bernoulli number”,2013 University of Minnesota
- Luigi Manabrea, con traduzione e note di Ada Lovelace, “Sketch the analitycal engine invented by Charles Babbage”,1842,Ginevra
- Stephen Wolfram,”Untangling the tale of Ada Lovelace”,2015
- Terotil “Ada’s Bernoulli Number Function”,2017
- Silvio Henin, “Augusta Ada Lovelace (1815-1852)”,2015
[1] Disponibile in inglese n.5 in bibliografia
[2] nel 2015 rinominato “Blanka~it.wiki” per ragioni di omonimia tra gli utenti delle diverse versioni linguistiche
[3] Le varie versioni linguistiche di questa enciclopedia digitale sono del tutto autonome e vi si possono trovare grosse differenze nei contenuti delle voci corrispondenti.
[4] Per esempio vedi n.3,n.4 in bibliografia