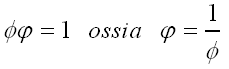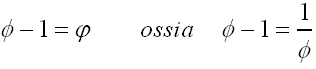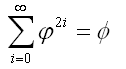una mattina

Riflessioni filosofico matematiche
sul tema della fiaba di Re Aureo

Al tempo del suo massimo splendore Re Aureo aveva il lato minore di 1 unità regia ed il lati maggiore 1.618033988749895... espresso in questa stessa unità. In seguito il re, preso atto delle invasioni, svalutò progressivamente la propria unità associandola al lato minore in perpetua diminuzione. Noi invece continueremo a misurare riferendoci a quella che c'era prima dell'invasione.

Dunque l'area del era 1x1.618033988749895...cioè 1.618033988749895...unità regie quadrate. Sia il lato maggiore che l'area del Re erano espresse dallo stesso numero aureo che per brevità si indica con f.

Ricapitolandola situazione iniziale:
lato minore 1 lato maggiore f, area f

Il primo degli invasori era un quadrato di lato 1 ed area 1
Dunque dopo la prima invasione l'area regia diventò f-1.
Il lato maggiore che era f ora è 1 dunque ha subito una moltiplicazione per 1/f = 0.618033988749895...
cioè una riduzione vicina al 62%
Chiamiamo per semplicità questo numero con j.
Notiamo che f e j sono numeri inversi nella moltiplicazioni ossia, come si dice, reciproci.
Infatti risulta

Dato che dopo l'invasione il rapporto tra i lati non cambia anche il lato minore deve aver subito un'identica riduzione essendo essendo stato moltiplicato per j. Siccome valeva 1 ora sarà esattamente j.
Quindi le nuove dimensioni dopo l'invasione del primo quadrato (fase 1) sono j e 1 e la nuova area è j.
Dato che ovviamente i due modi per calcolare l'area devono dare lo stesso risultato sarà:

Ricapitolando l'invasione di un quadrato causa la riduzione dei lati del Re aureo di un fattore j
Ecco dunque una tabella che mostra come variano le dimensioni ad ogni invasione:

fasi	lato minore Re	lato maggiore Re	area Re	lato invasore	area invasore
0	1	f	f	-	-
1	j	1	j	1	1
2	j²	j	j³	j	j²
3	j³	j²	j⁵	j²	j⁴
4	j⁴	j³	j⁷	j³	j⁶
5	j⁵	j⁴	j⁹	j⁴	j⁸
6	j⁶	j⁵	j¹¹	j⁵	j¹⁰
...	^...	^...	^...	^...	^...

Ecco allora l'area dell'esercito degli infiniti gnomoni quadrati:

1+j²+j⁴+j⁶+j⁸+j¹⁰+j¹²+j¹⁴+j¹⁶+j¹⁸+j²⁰+.... e cosi via per infiniti addendi

Questa area potenziale, presumibilmente, sta ancora aumentando e non cesserà mai di farlo. Eppure d'altra parte, pur aumentando indefinitamente, avrà una crescita limitata non potendo mai superare f l'area originale dell'antico regno. Questa sembra essere una fortuna per il nostro Re che, quindi, non dovrebbe mai scomparire.

Eppure, quando dalla potenza si passerà all'atto, quella somma di infiniti termini, per quanto strano possa sembrare, perderà il suo favoloso dinamismo per un risultato statico che sarà, con buona pace del Re, esattamente f