|
Il merletto di Koch tradizionale |
 |
| Il segmento unitario viene trasformato iterando la sostituzione di un intero con 4/3 dello stesso con angolo acuto di 60 gradi |
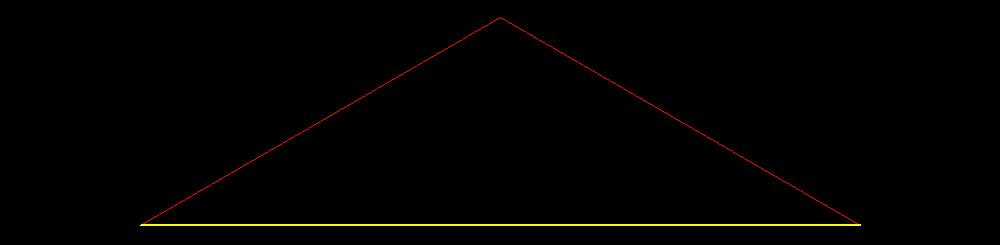 |
| Livello 0: un segmento in giallo. Sullo sfondo in rosso un triangolo equilatero con rapporto radice di tre tra lato maggiore e minore. |
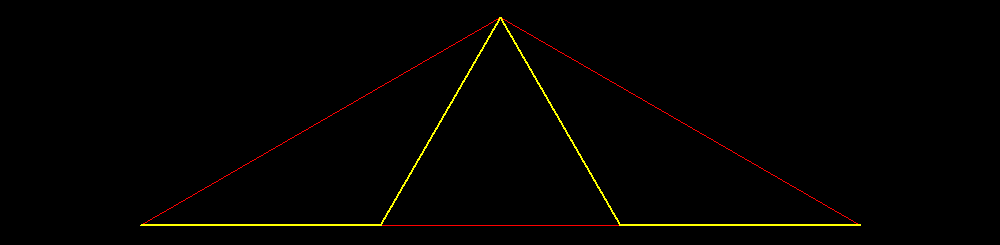 |
| Livello 1: Prima sostituzione (in giallo, il triangolo rosso di riferimento rimane fisso). Si ottengono 4 segmentini di lunghezza 1/3. |
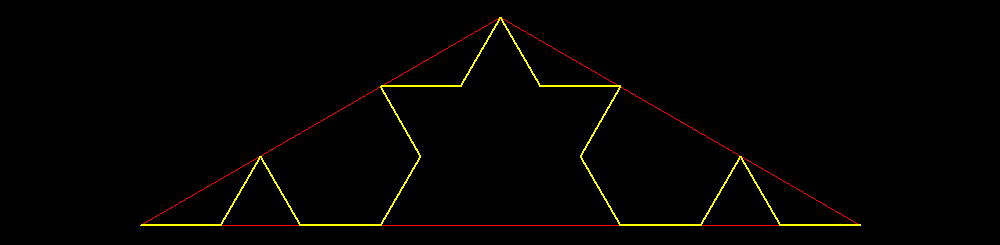 |
| Livello 2: Seconda sostituzione estesa ai 4 segmenti precedenti. Si ottengono 16 segmentini di lunghezza 1/9. |
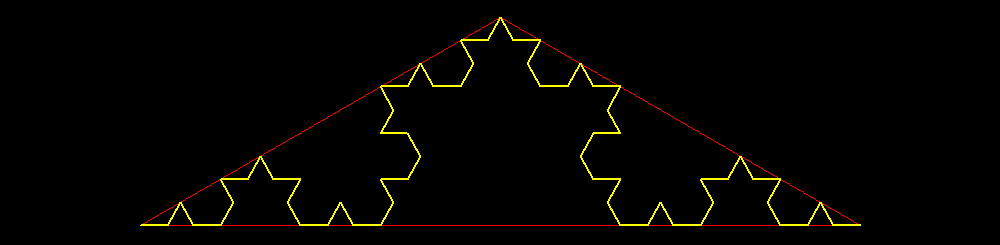 |
| Livello 3: Terza sostituzione estesa ai 16 segmenti precedenti. Si ottengono 64 segmentini di lunghezza 1/27. |
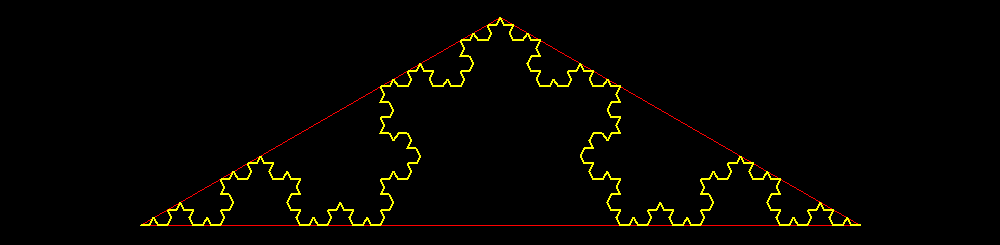 |
| Livello 4: Quarta sostituzione estesa ai 64 segmenti precedenti. Si ottengono 256 segmentini di lunghezza 1/81. |
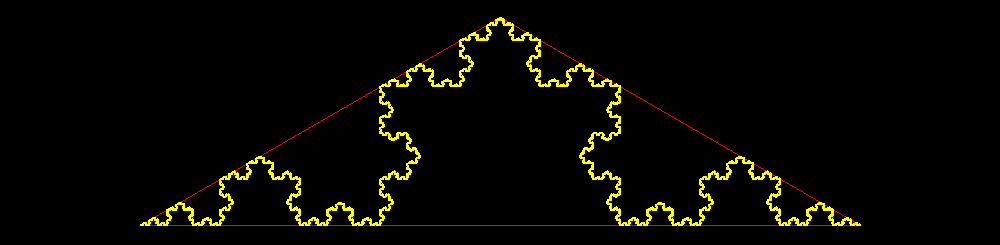 |
| Livello n: Si ottengono 4n segmentini di lunghezza 1/3n. |
 |
| Livello infinito: Passando dall'infinito potenziale a quello attuale si ottiene la famosa curva non derivabile scoperta dal matematico svedese Helge von Koch (1870-1924). Al crescere di n il perimetro č 4n/3n cresce oltre ogni limite quindi la lunghezza di questa curva infinitamente frastagliata č infinita. |
|
|
| Le tre finestre dell'MSWLogo sulla sfondo della pagina wikipedia dedicata a Koch. Nella finestra Editor le istruzioni per la tartaruga. Nella finestra Commander il comando per ottenere la curva che la tartaruga descrive nella finestra MSWLogo screen |
|
Se non avete ancora
MSWLogo
potete scaricarlo dal sito della Softronix oppure
cliccando qui. Per avere il programmino curvaKoch potete copiarlo oppure scaricarlo cliccando qui Il programma, scaricabile in formato zip, appena decodificato in formato LGO e caricato con "load" nel MSWLogo eseguirā automaticamente la lista di comandi assegnati mediante "make" alla variabile speciale "startup" leggibile nell'edit dopo i normali comandi per la tartaruga implementati dall'utente. Per il significato dei comandi utilizzati vedere anche il vocabolario animato del Tartapelago. |