Fiocco di neve siamese generato dal rombo equilatero (angoli 60 e 120 gradi)
per iterazioni successive di merletti di Koch estroversi

Animazione esplicativa 
Livello 0. Rombo unione di due triangoli equilateri. Poligono equilatero di 4 lati. Lunghezza lato: 1 (unitā di misura lineare) . Perimetro 4. Area:  2 (unitā di misura della superficie mezzo rombo. Se anche per l'area si volesse invece mantenere l'unitā lineare allora i valori delle aree indicati qui e di seguito andrebbero moltiplicate per 1/4 della radice di tre, area di un singolo triangolino equilatero).    Livello 1. Poligono equilatero di 16 lati. Lunghezza di un lato: 1/3. Perimetro 16/3. Area 22/9 (alla precedente si aggiungono 4 piccoli equilateri di area 1/9)
Livello 2. Poligono equilatero di 64 lati. Lunghezza di un lato: 1/9. Perimetro 64/9. Area  214/81 (al precedente si sommano 42 piccoli equilateri di area 1/92) Livello 3. Poligono equilatero di 256 lati. Lunghezza di un lato: 1/27. Perimetro 256/27. Area  ... (alla precedente, si sommano 43 piccoli equilateri di area 1/93)
Livello n. Poligono equilatero di 4n lati. Lunghezza di un lato: 1/3n. Perimetro 4n/3n. Area  ,,, (al precedente si sommano 4n piccoli equilateri di area 1/9n) Livello infinito. All'infinito, passando al limite, si ottiene il fiocco siamese. Lunghezza di un lato: infinitesima. Perimetro infinito. Area, sommando infiniti termini di una progressione geometrica di ragione 4/9, č 14/5,

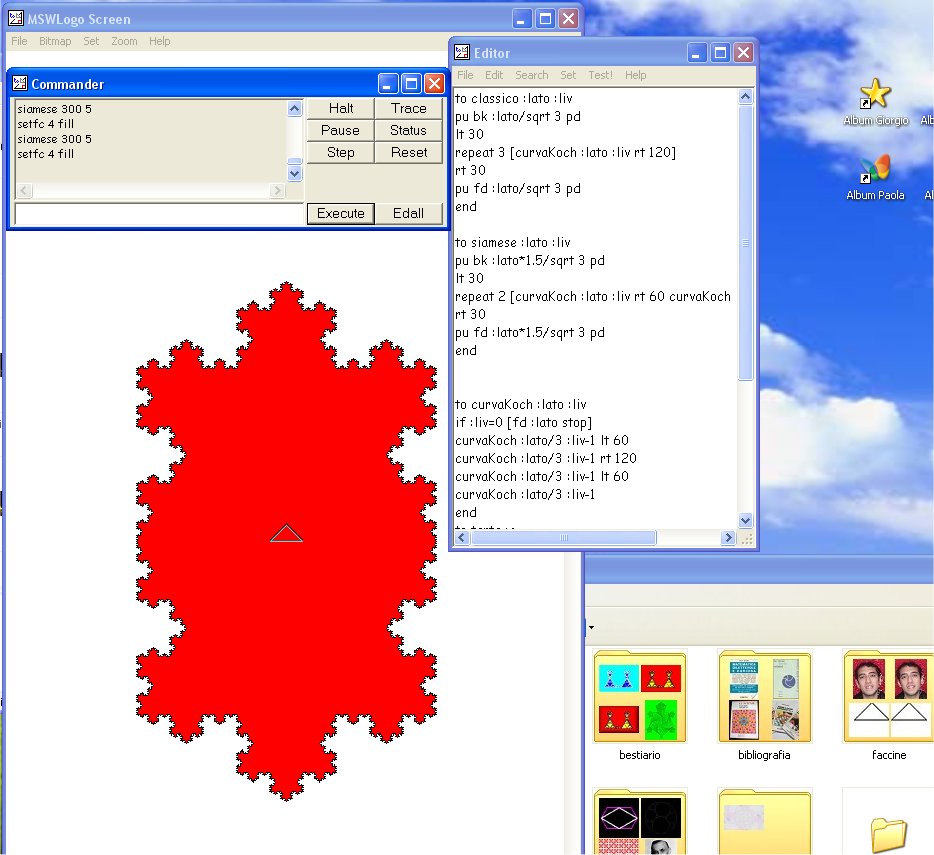
Le tre finestre dell'MSWLogo sulla sfondo di Windows. Nella finestra Editor le istruzioni per la tartaruga. Nella finestra Commander il comando per ottenere il siamese  che la tartaruga disegna nella finestra MSWLogo screen

Se non avete ancora MSWLogo potete scaricarlo dal sito della Softronix oppure cliccando qui.
Per avere il programmino potete copiarlo oppure scaricarlo cliccando qui
Il programma, scaricabile in formato zip, appena decodificato in formato LGO e caricato con "load" nel MSWLogo eseguirā automaticamente la lista di comandi assegnati mediante "make" alla variabile speciale "startup" leggibile nell'edit dopo i normali comandi per la tartaruga implementati dall'utente. Per il significato dei comandi utilizzati vedere anche il vocabolario animato del Tartapelago.