|
Confronto tra due convergenze al fiocco classico |
|
 |
|
| Animazione esplicativa | |
 |
 |
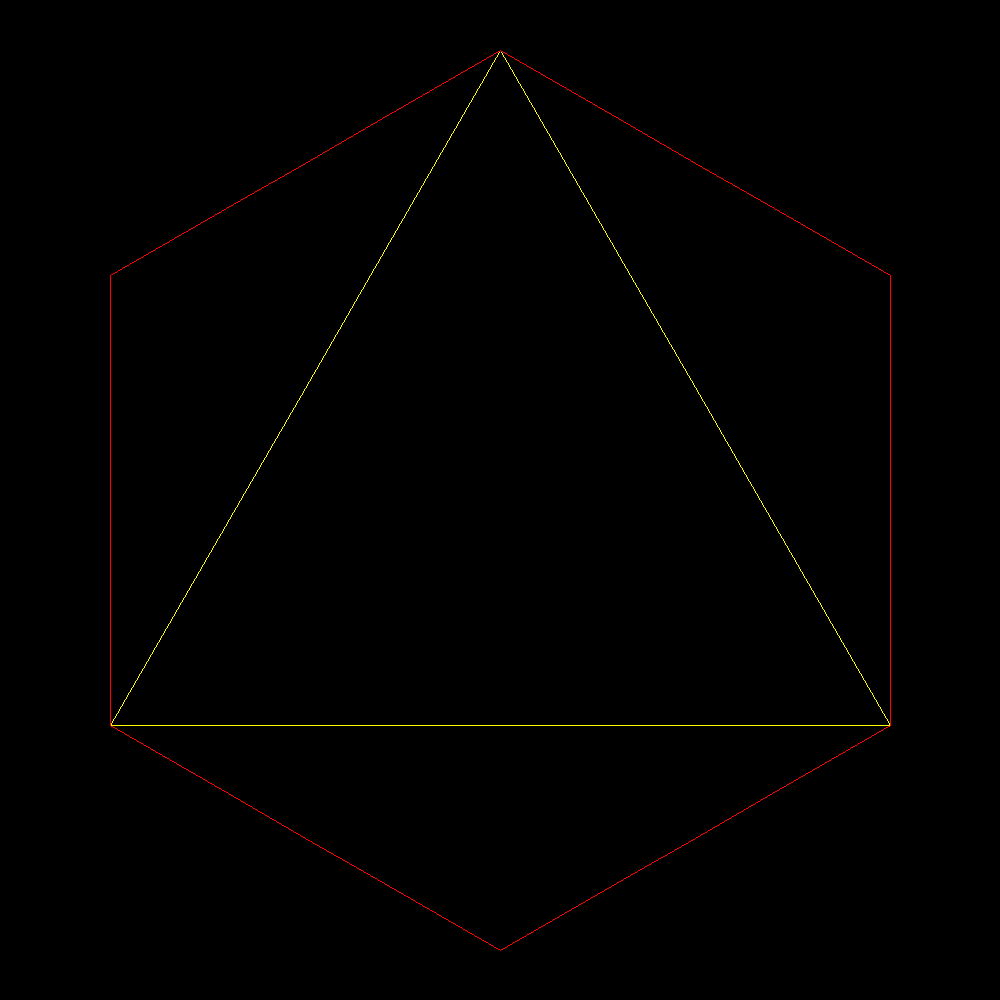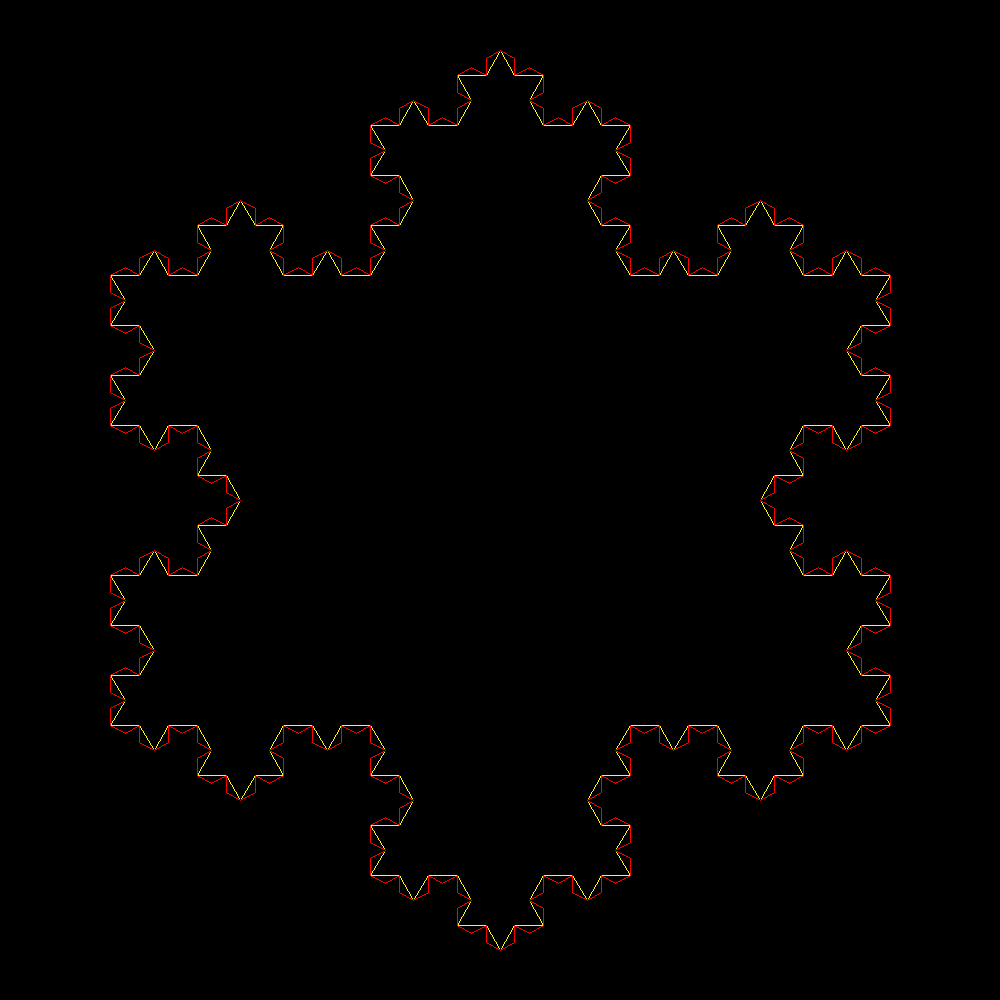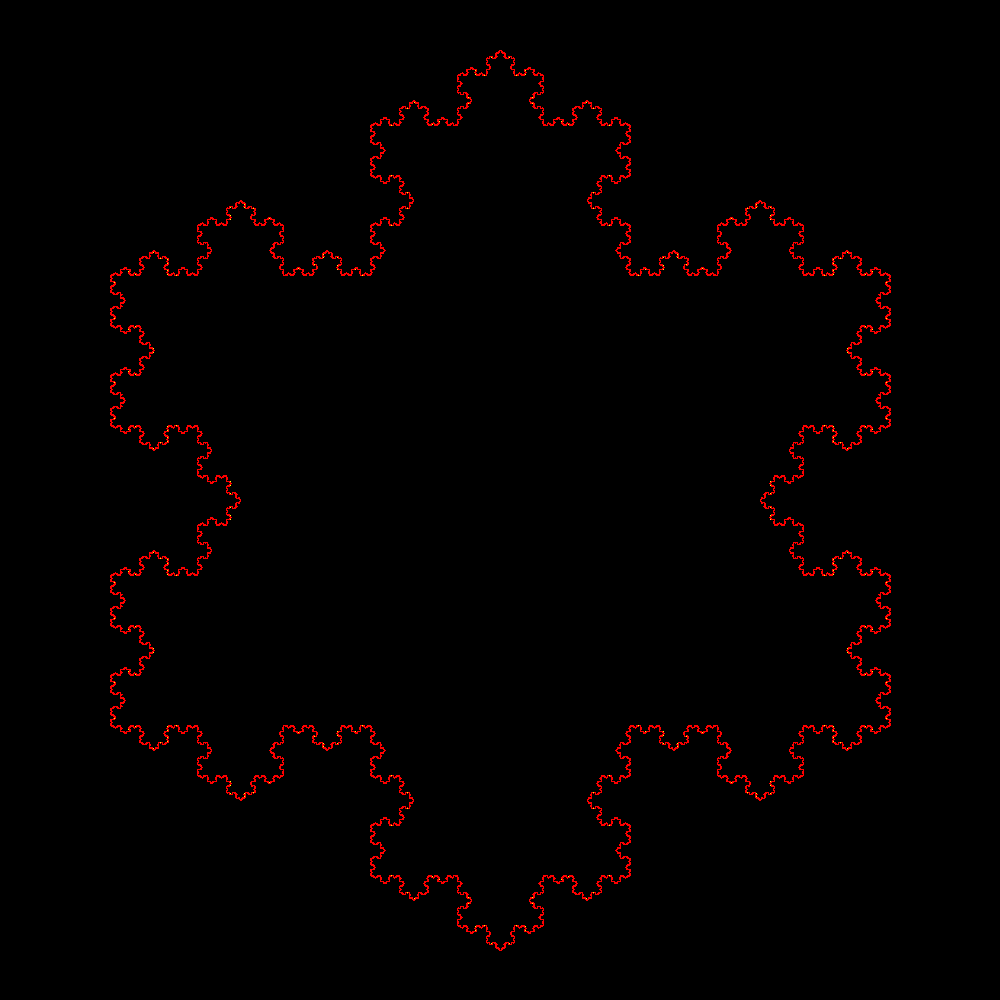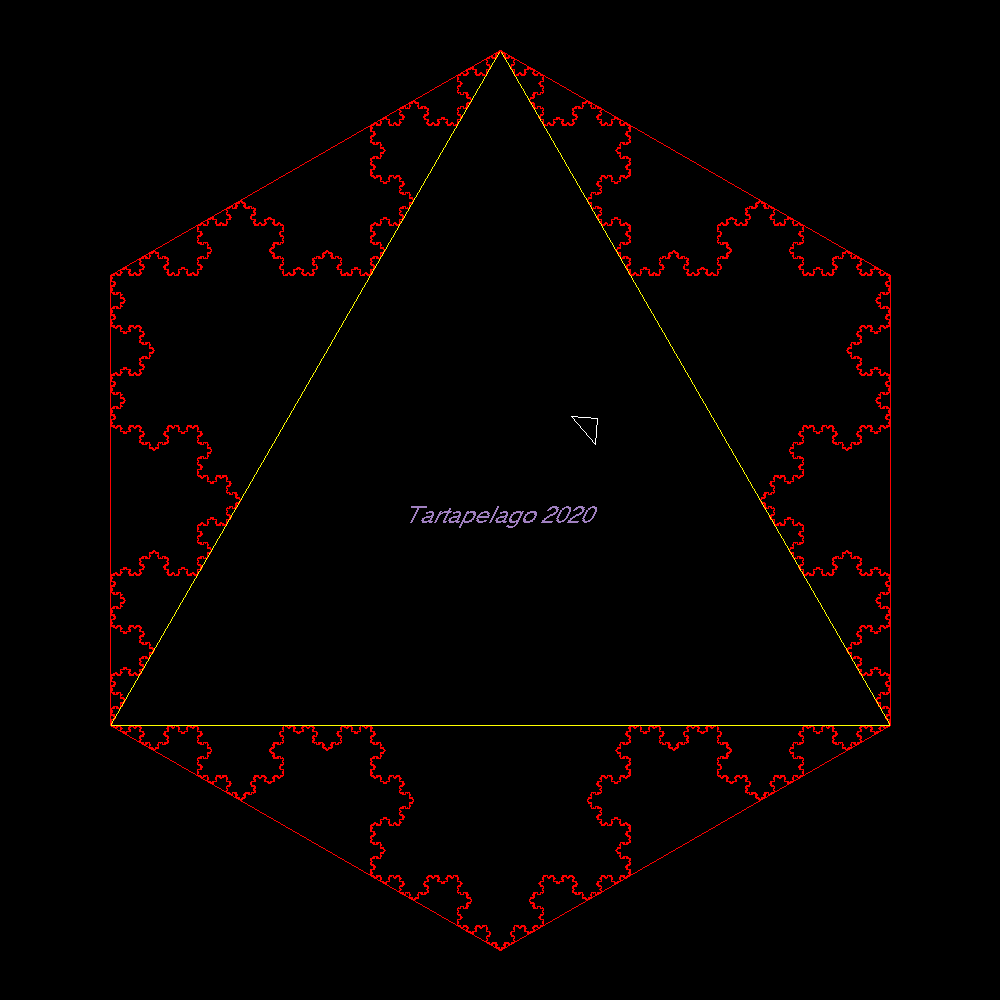
| Livello 0. Triangoli in nero 3. Area tra i due poligoni: 3 (unità area triangolo isoscele) | Livello 1. Triangoli 12. Area tra poligoni 12/9 |
 |
 |
| Livello 2. Triangoli 48. Area tra poligoni 48/81 | Livello 3. Triangoli 192. Area tra poligoni 192/729 |
 |
 |
| Livello n. Triangoli 3*4n. Area tra poligoni 3*4n/9n | Livello infinito. Area tra poligoni 0 |
 |
 |
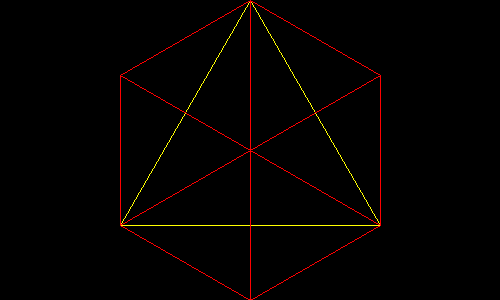
| Precedentemente per comodità visiva avevamo fatto delle scelte. Preso il piccolo triangolo equilatero (in rosso nella figura sopra) come unità di misura l'esagono regolare aveva area sei. Preso il grande triangolo equilatero giallo come unità di misura lo stesso aveva area 1. Mantenendo la prima unità di misura invece avrebbe area 3 dato che ogni triangolo giallo è formato da 6 metà del rosso e quindi è equivalente a tre equilateri rossi. | Abbiamo visto che l'esagono di area 6 e il triangolo inscritto di area 3 generano lo stesso fiocco di Koch con un area intermedia pari a 24/5 del triangolo rosse unitario e (8/5 del giallo). SE invece si vuole usare l'unità lineare cioè il lato unitario del piccolo triangolino equilatero il valore 4,8 va moltiplicata per l'area di un singolo triangolino equilatero: (radice 3)/4 |