|
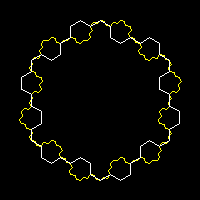
Fior d'esagono alternato [1/2] |
|||
|
Scissione eptagemellare speculare. Un frattale rep-7 (replicating tiles) |
|||
 |
|||
| La costruzione evidenzia come dopo ogni fase l'immagine si riduca linearmente per radice di sette e ruoti alternativamente a destra e a sinistra di un angolo di circa 19 gradi (arcsin (sqrt 21)/14). | |||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Nella prima riga in bianco la successione delle fasi pari (0,2,4,6). Nella seconda riga in giallo la successione delle fasi dispari(1,3,5,7) Nell'ultima infine la loro sovrapposizione che mostra la convergenza verso due frattali uguali ma inversi. Per far coincidere i due frattali limiti di queste due successioni sarebbe necessario un ribaltamento tridimensionale. | |||
 |
 |
||
| Il confronto evidenzia le lievi differenze tra il fior d'esagono alternato e il fior d'esagono continuo | |||
 |
|||
| Come si vede questi due frattali reciprocamente speculari sono replicanti (rep-tiles) di ordine 7, brevemente rep-7, e le sette figure congruenti figlie in cui si scindono sono copie ridotte e speculari dei loro rispettivi genitori. | |||