|
Plastic rectangle and Padovan sequence |
|
|
|
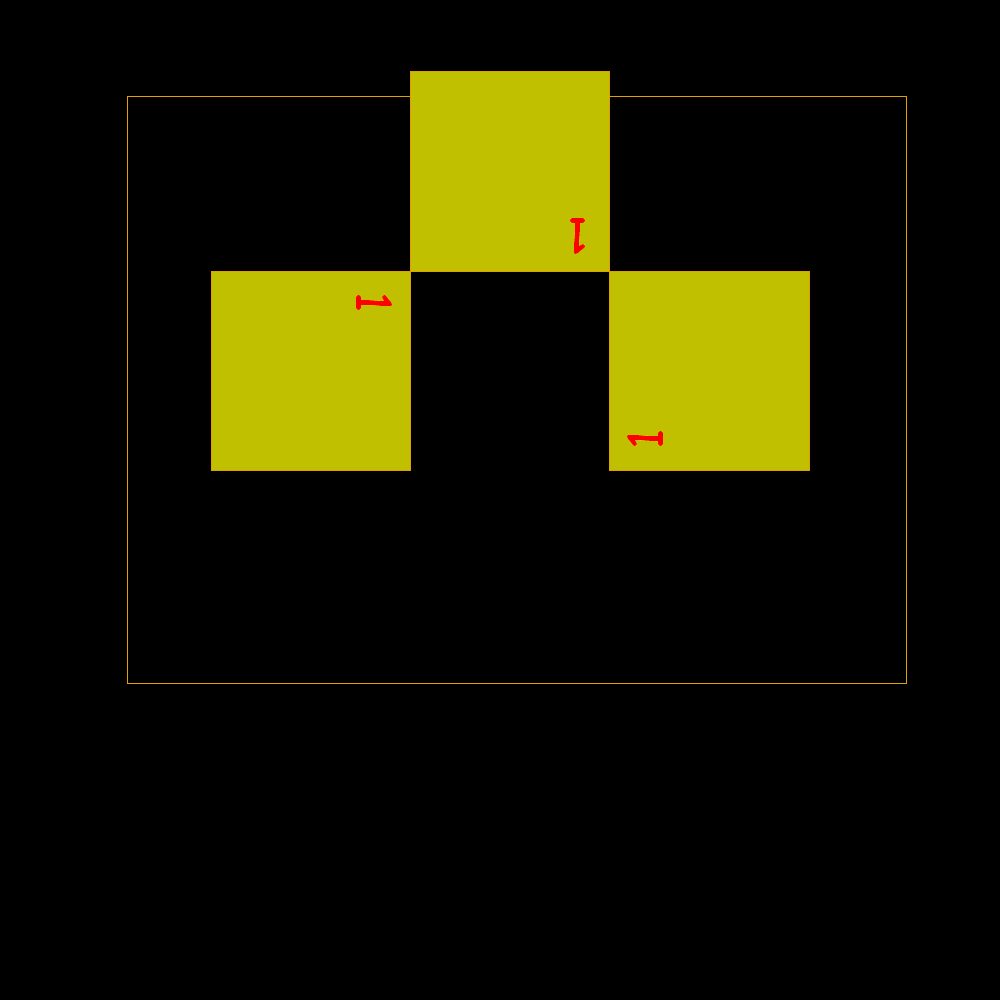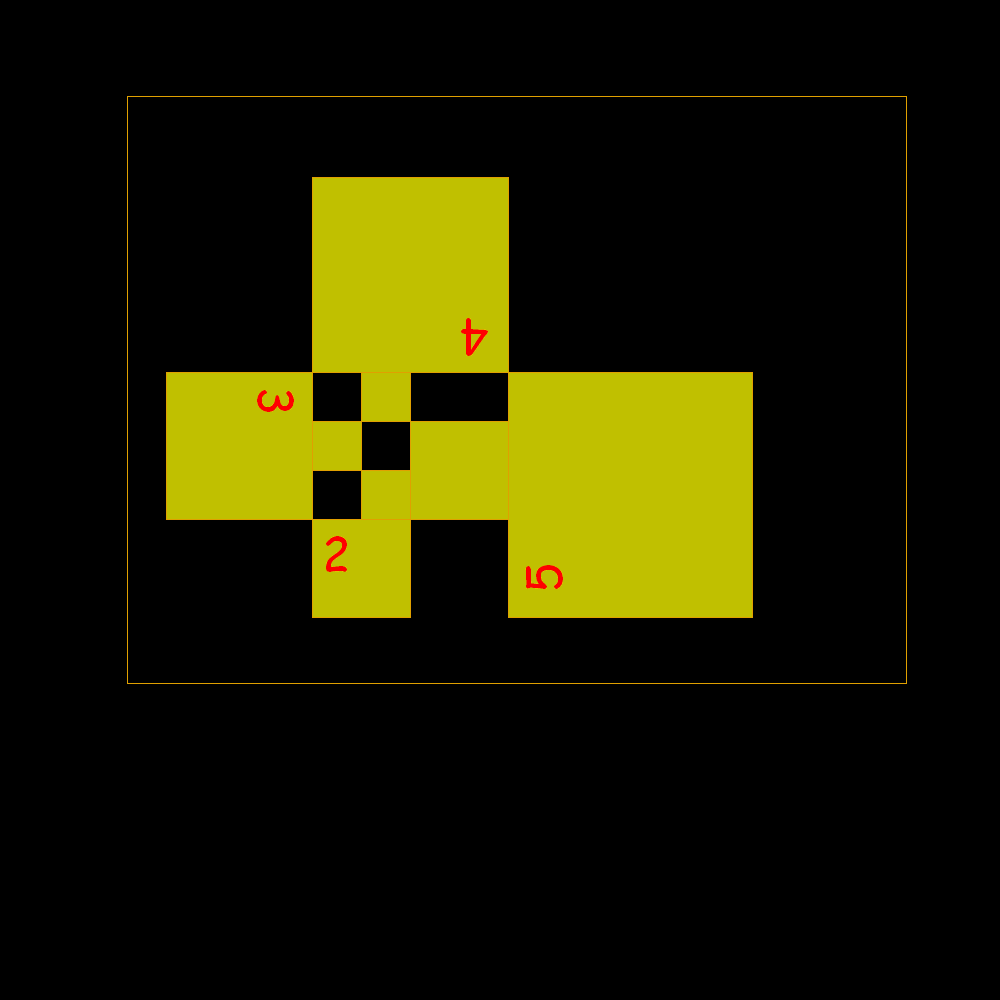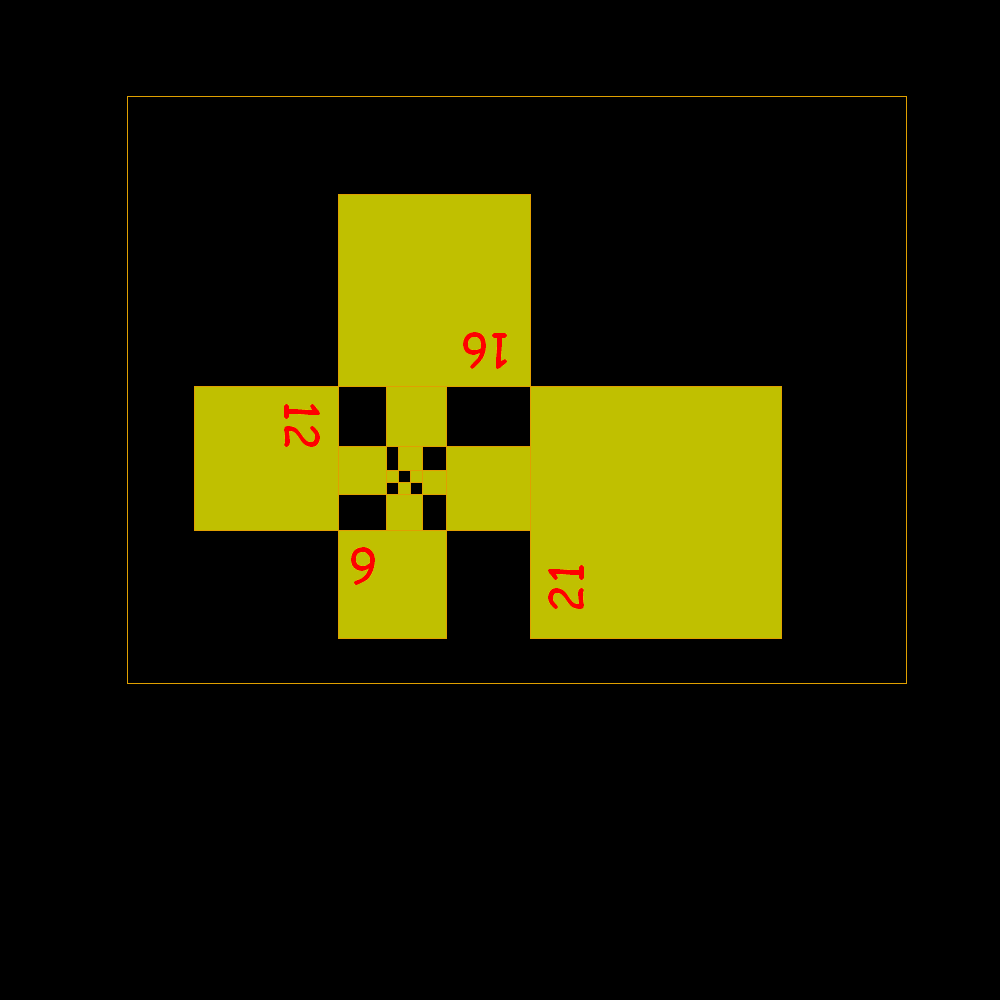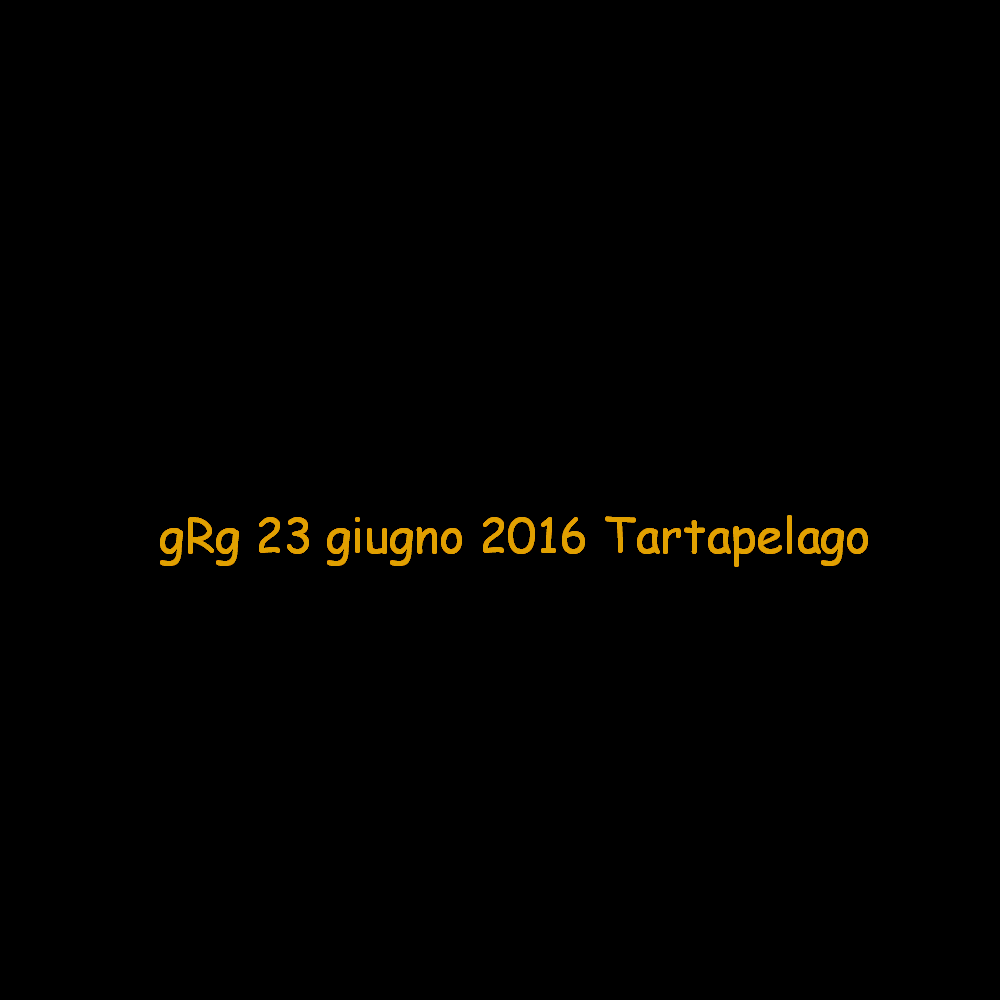
It
is observed that the side of a square equals the sum of the two not immediately
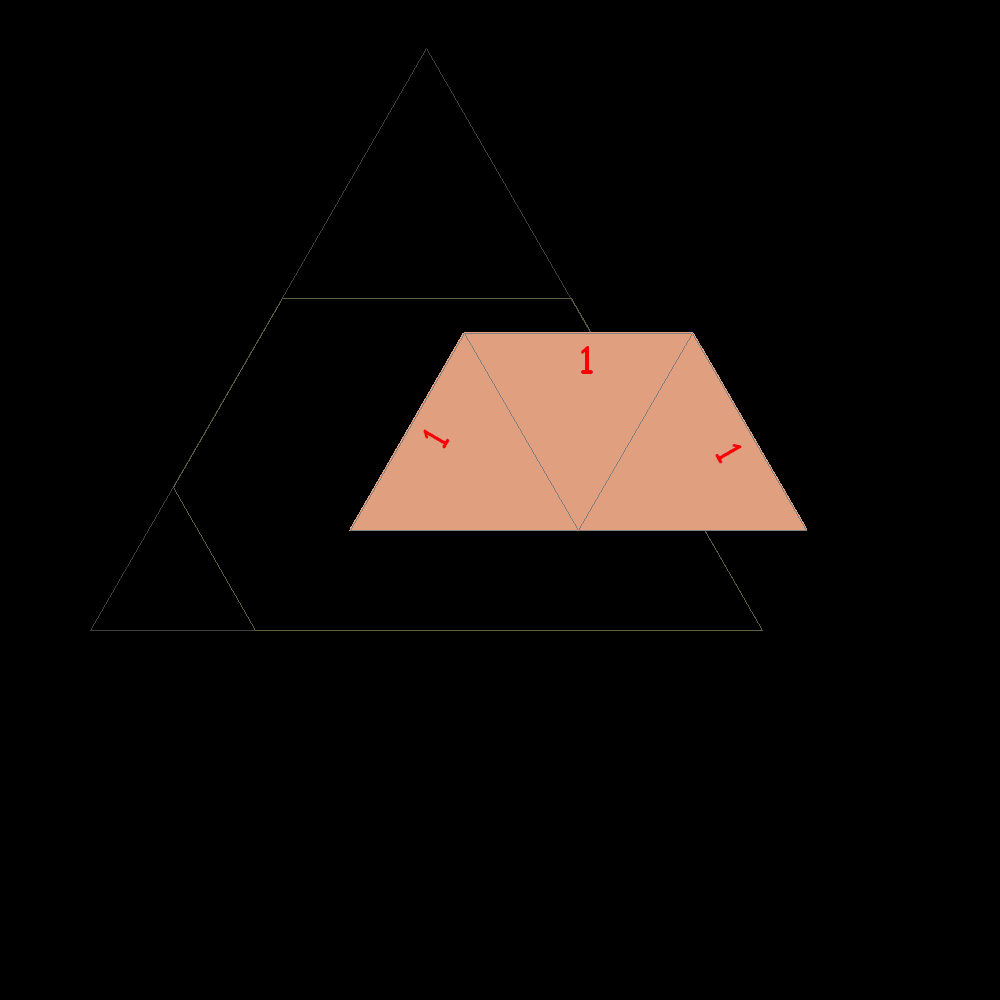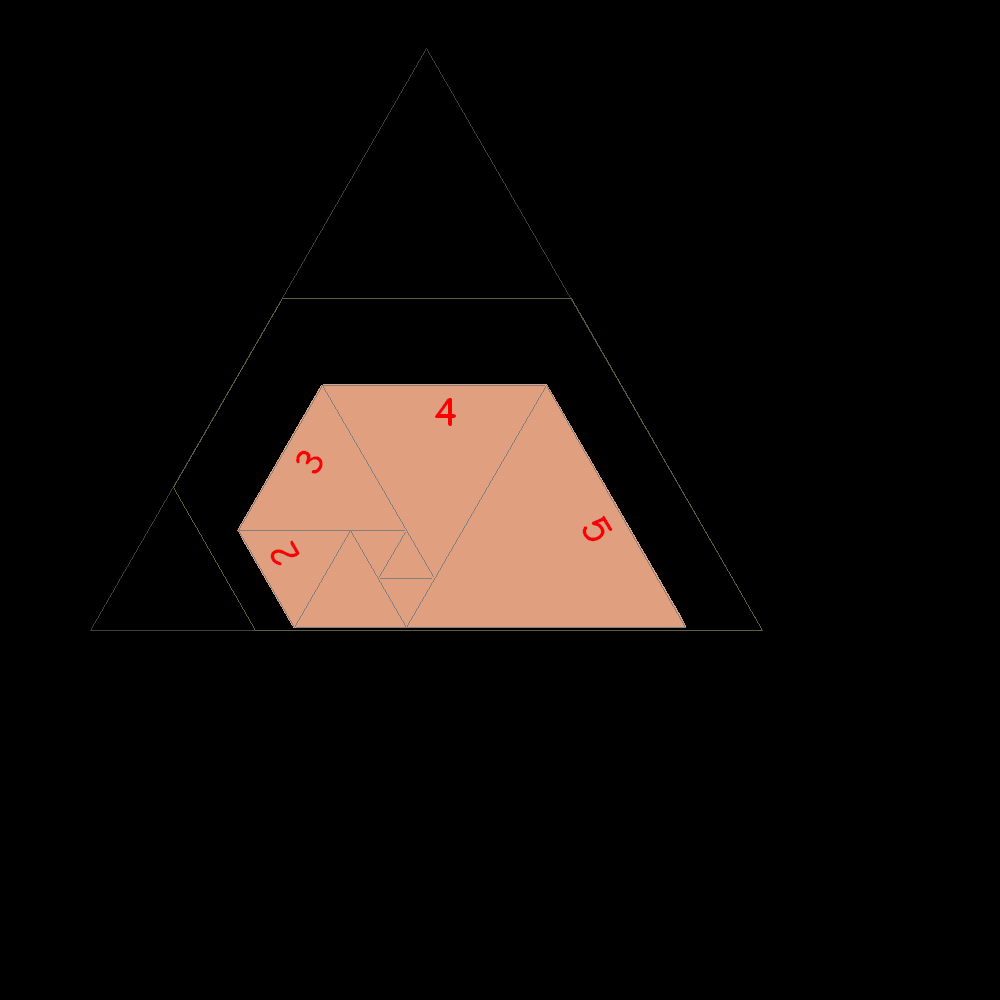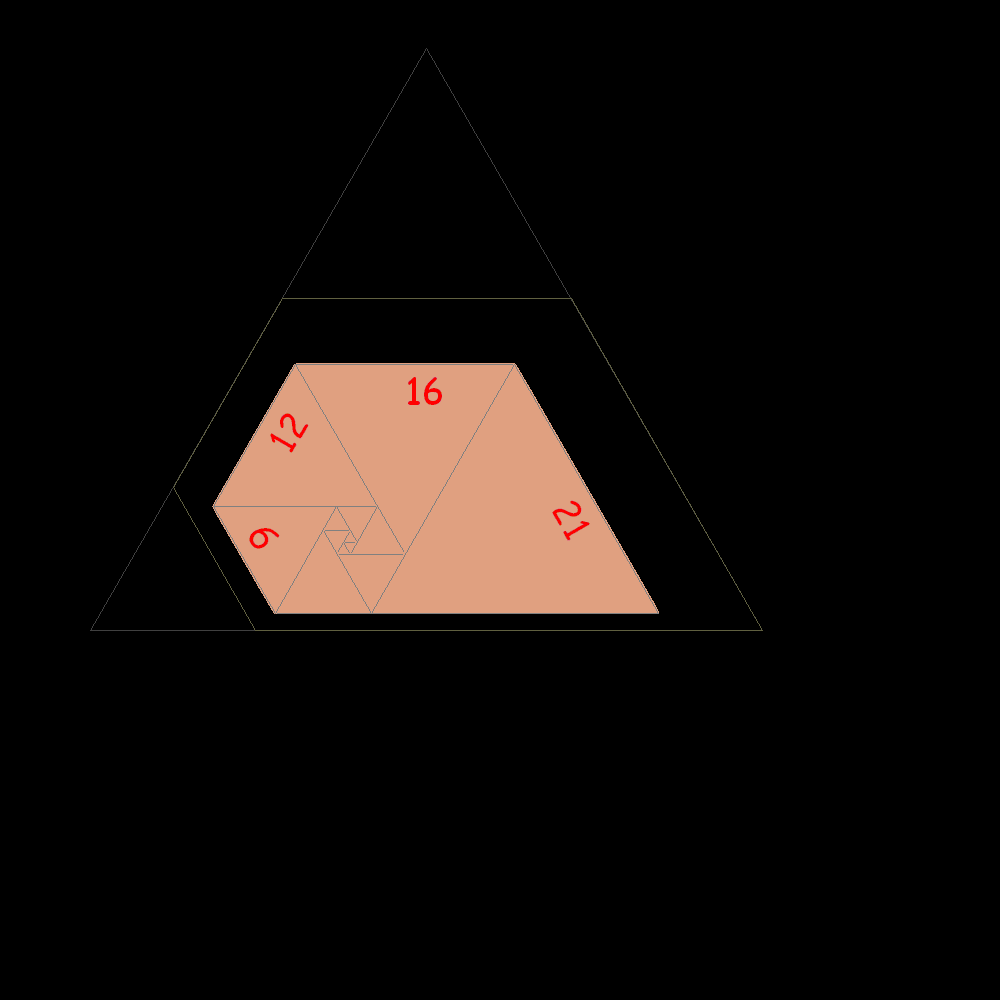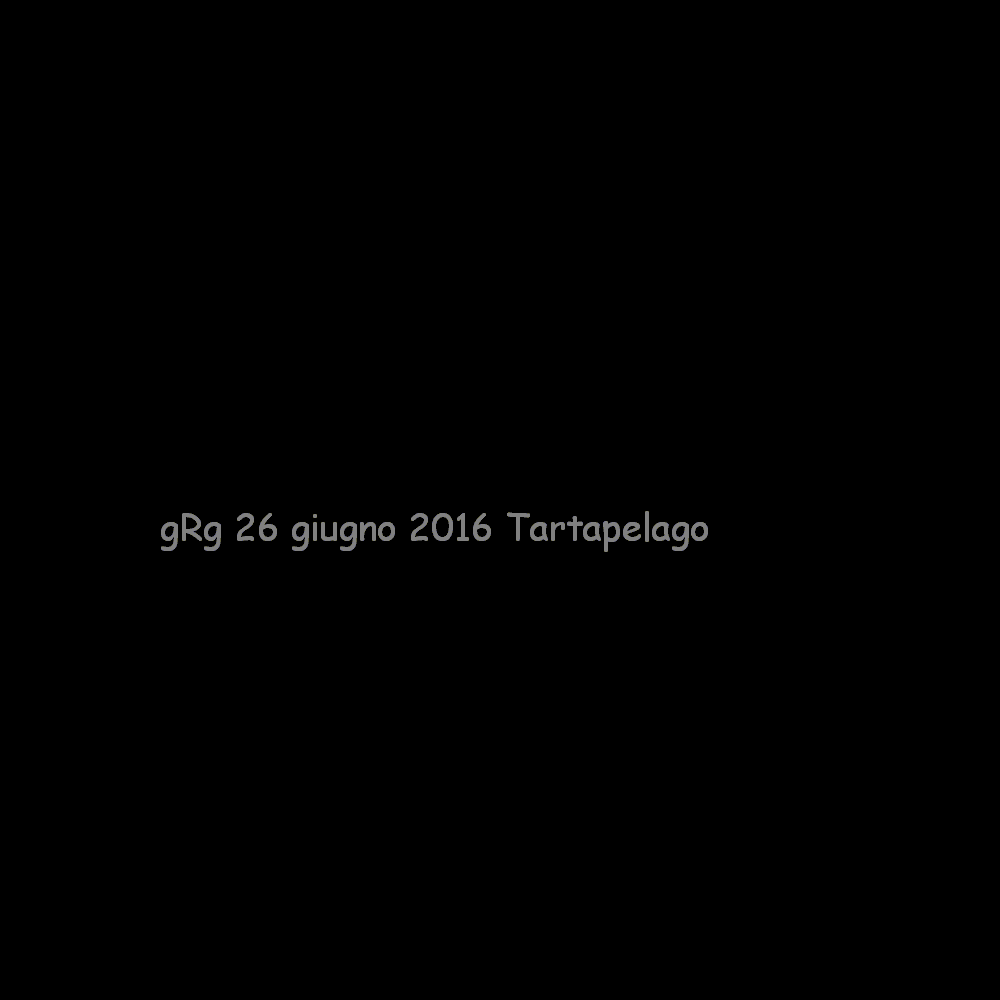
preceding. 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265, 351, 465, 616, 816, 1081,...
that it is the famous Padovan numbers (1/P=0.7548776662...one of the solutions of the following equation: r3+r2-1=0) |
 |
|
Start of rectangles identified by square building with sides according to the Padovan sequence |
 |
|
Shortly after the result is confused with the plastic rectangle to which it tends |
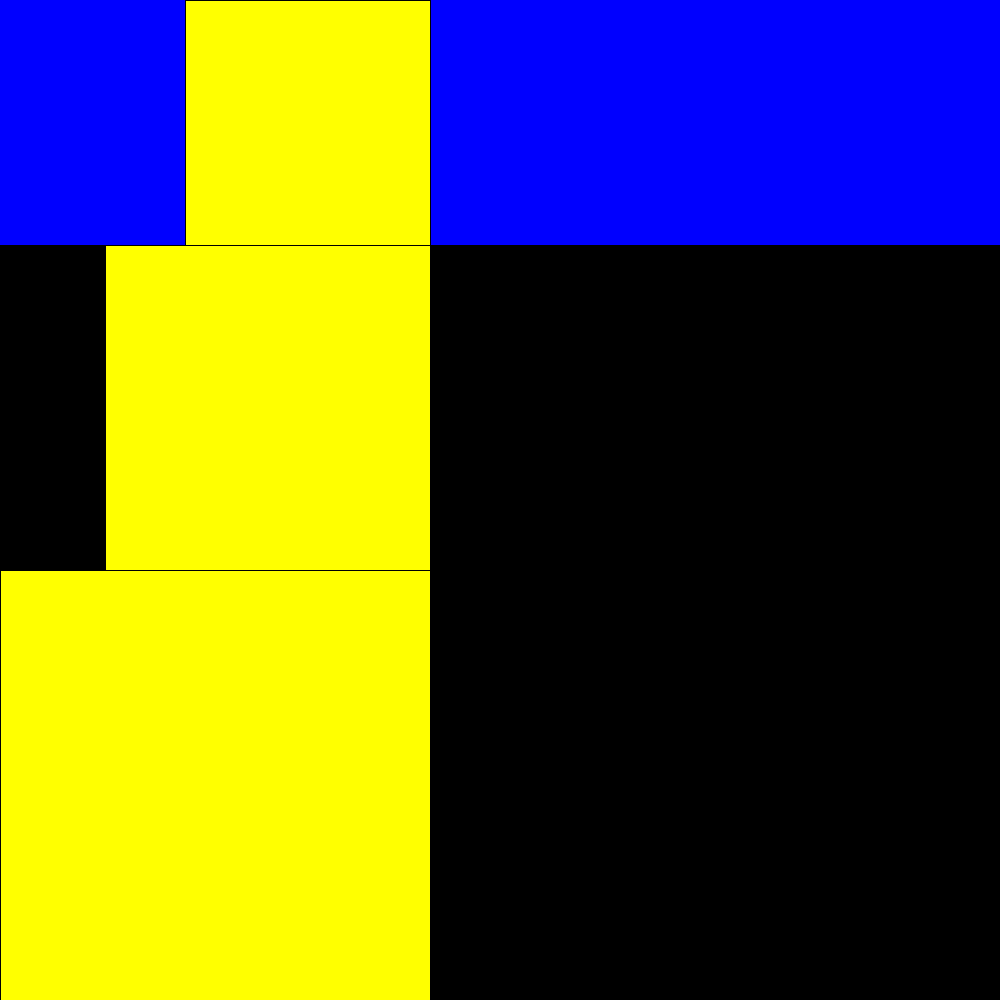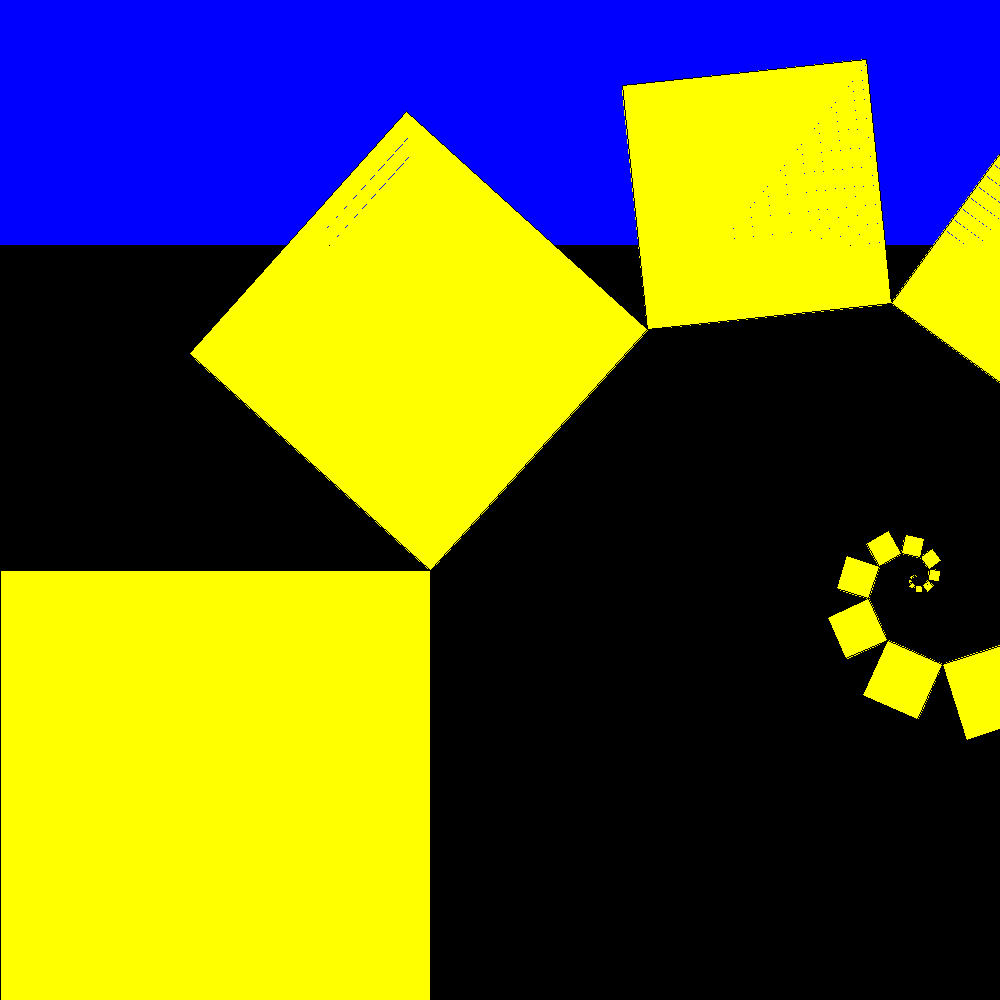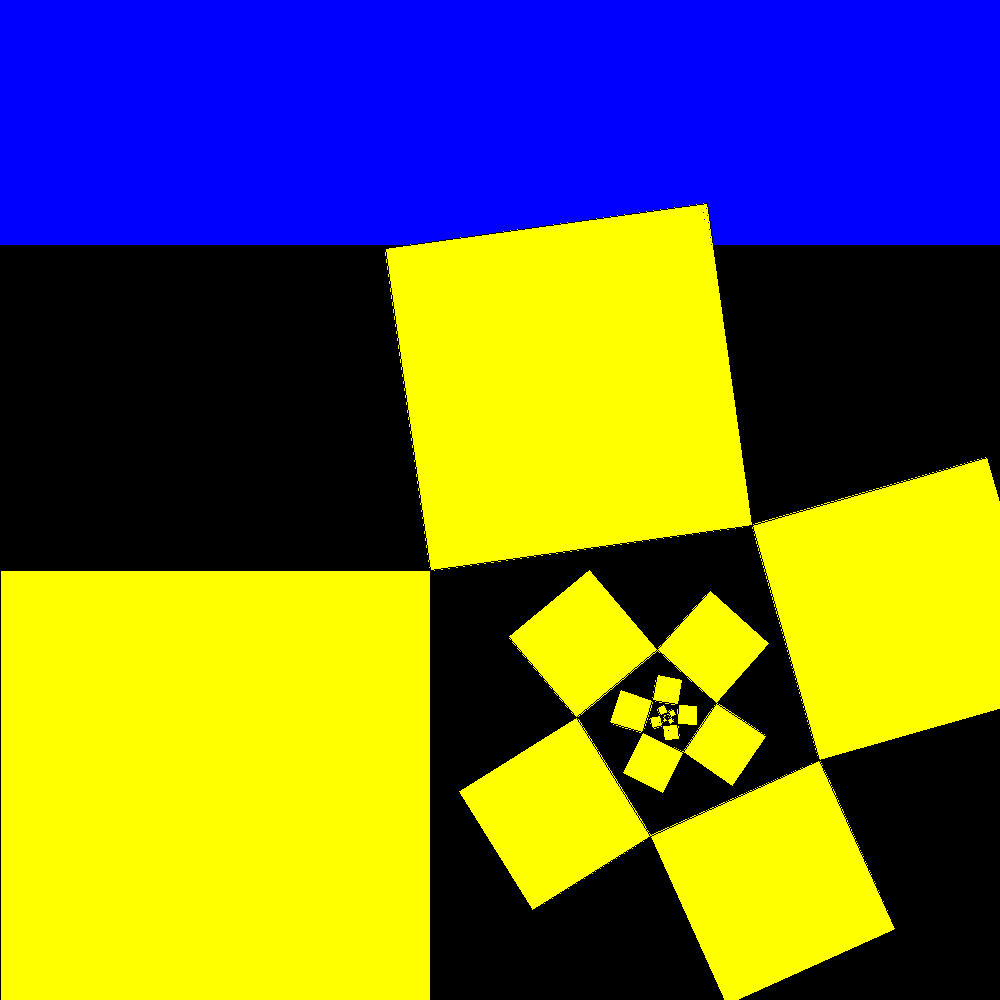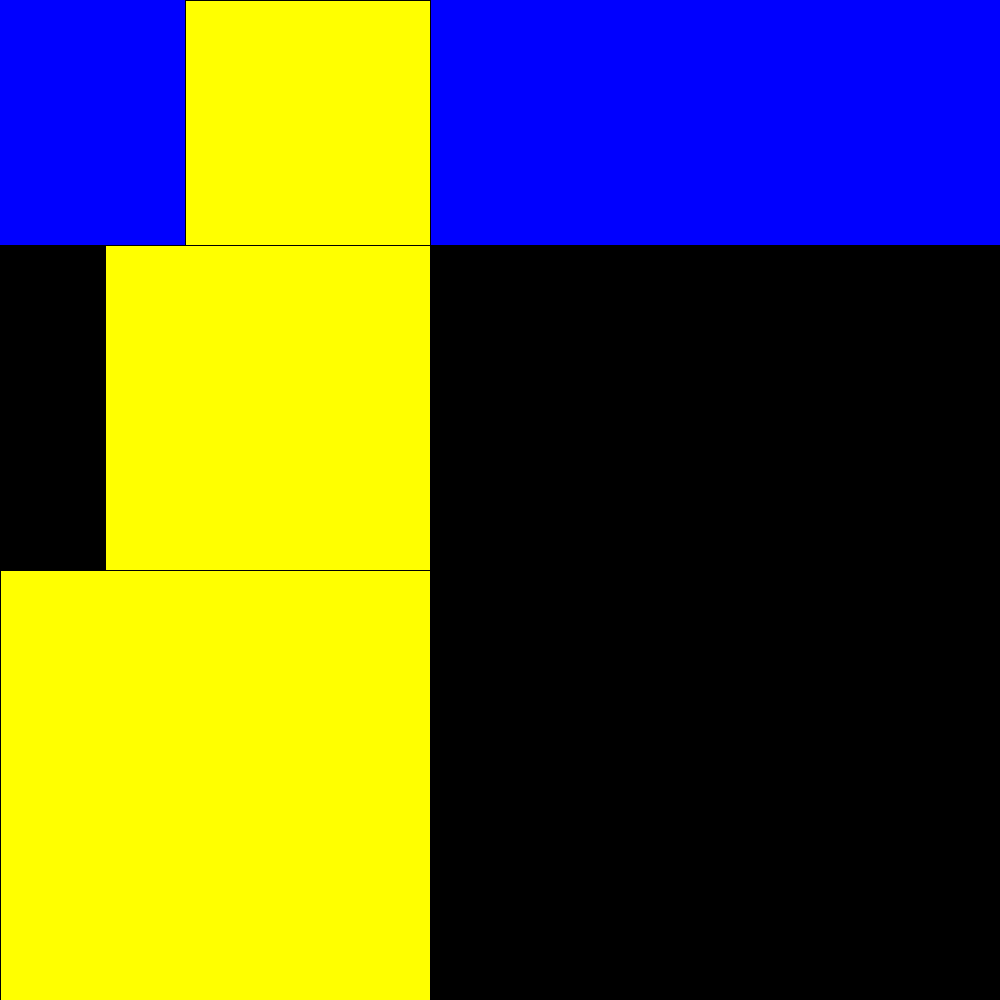 |
|
packing and unpacking |
 |
|
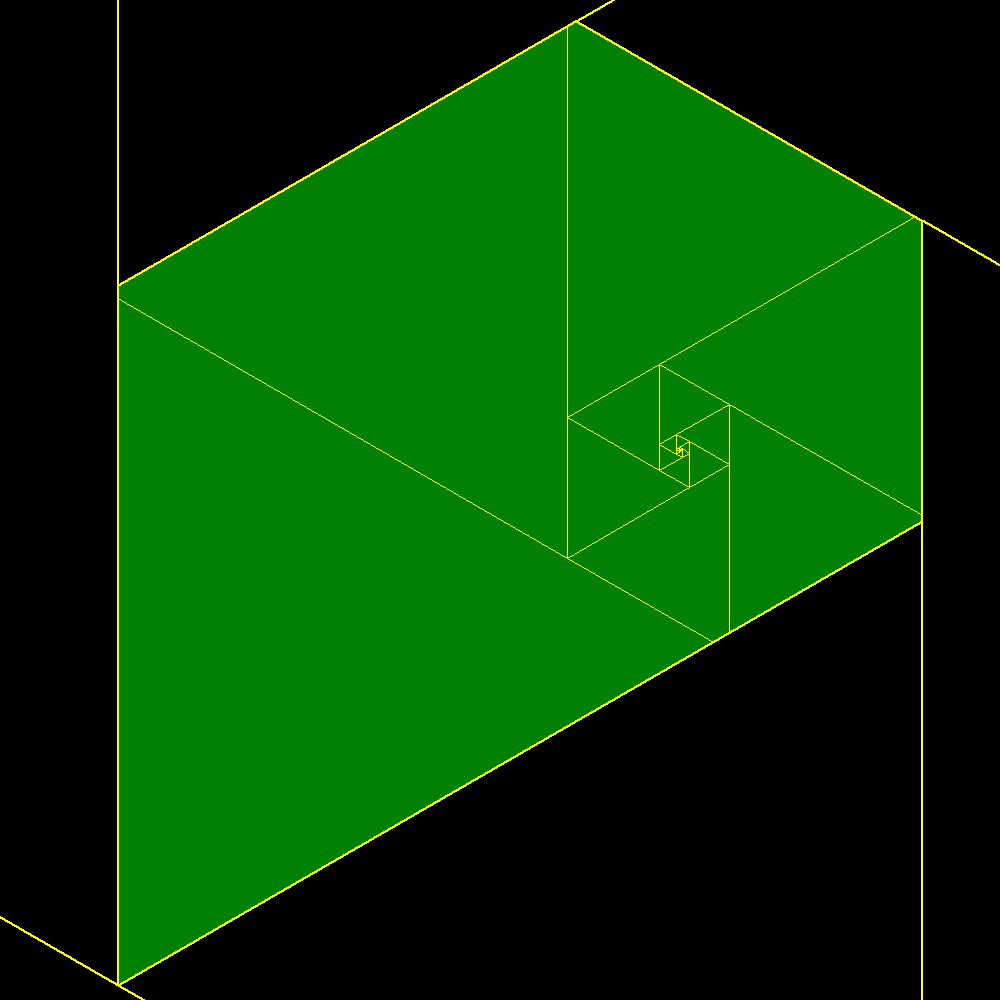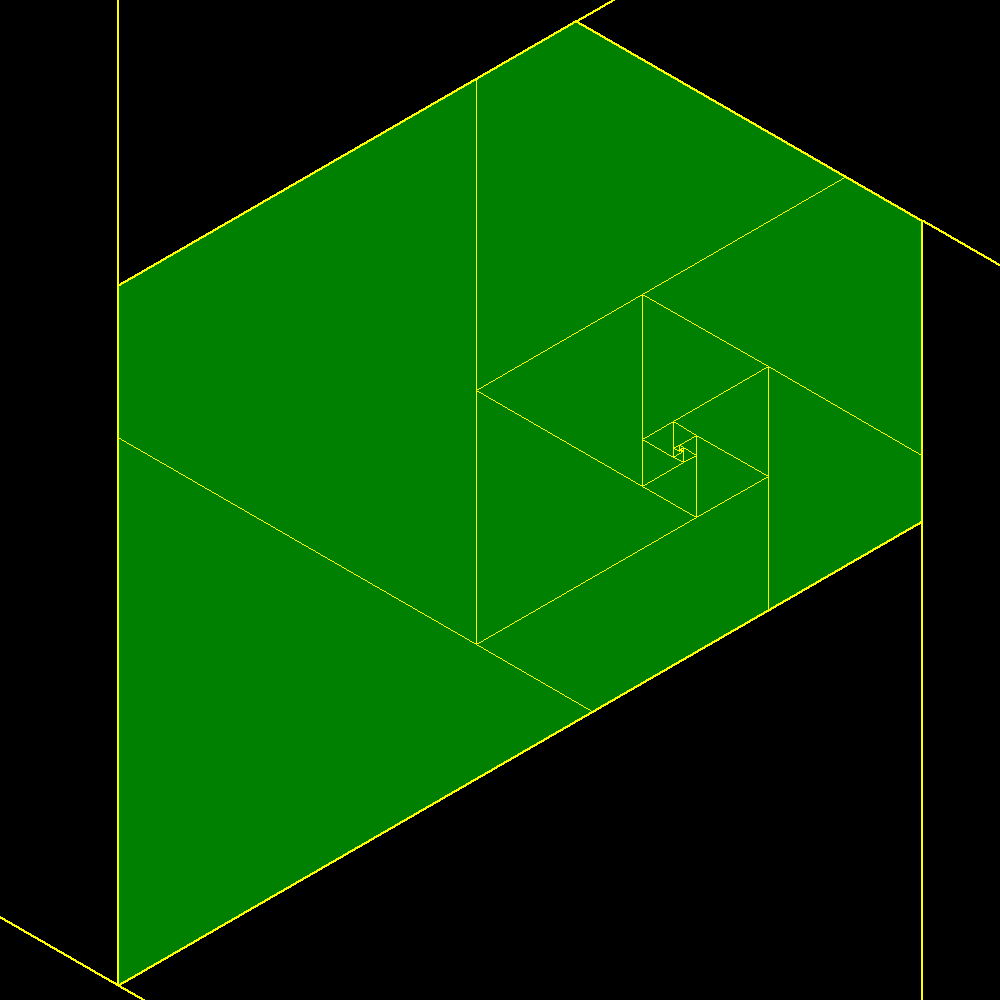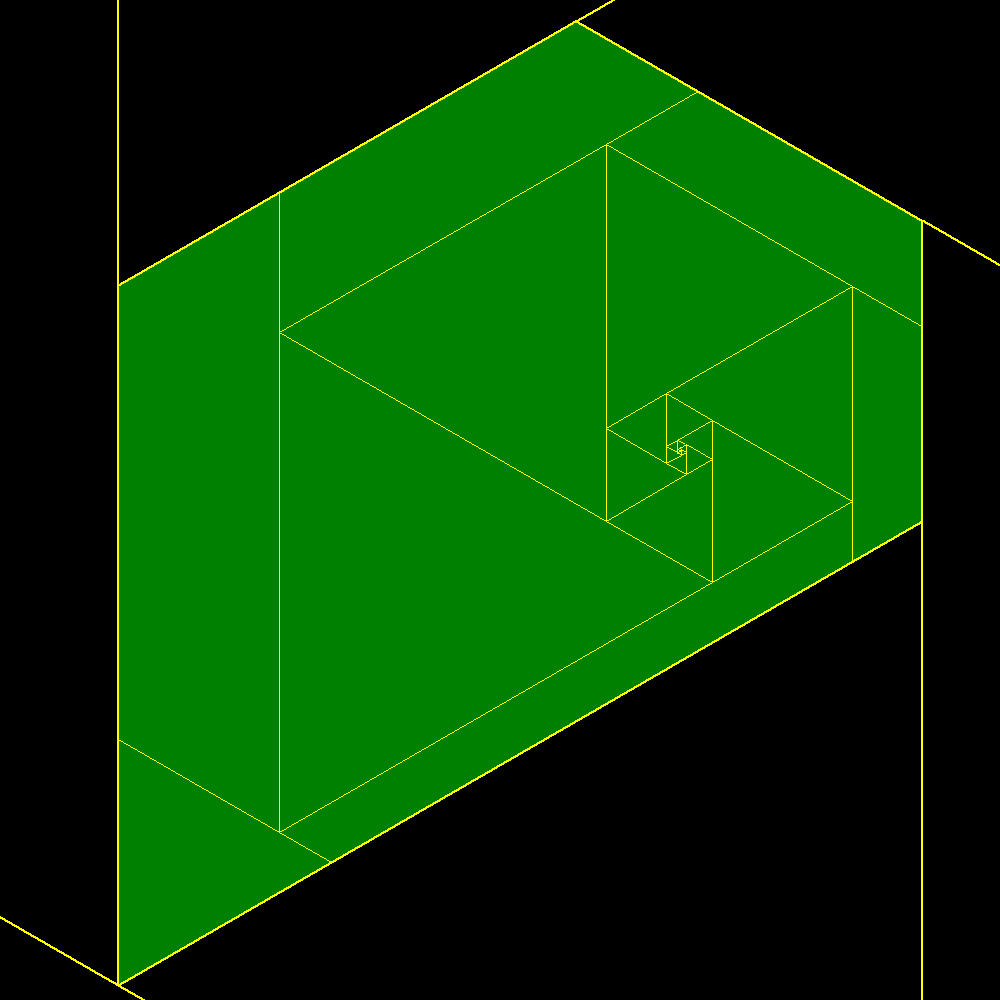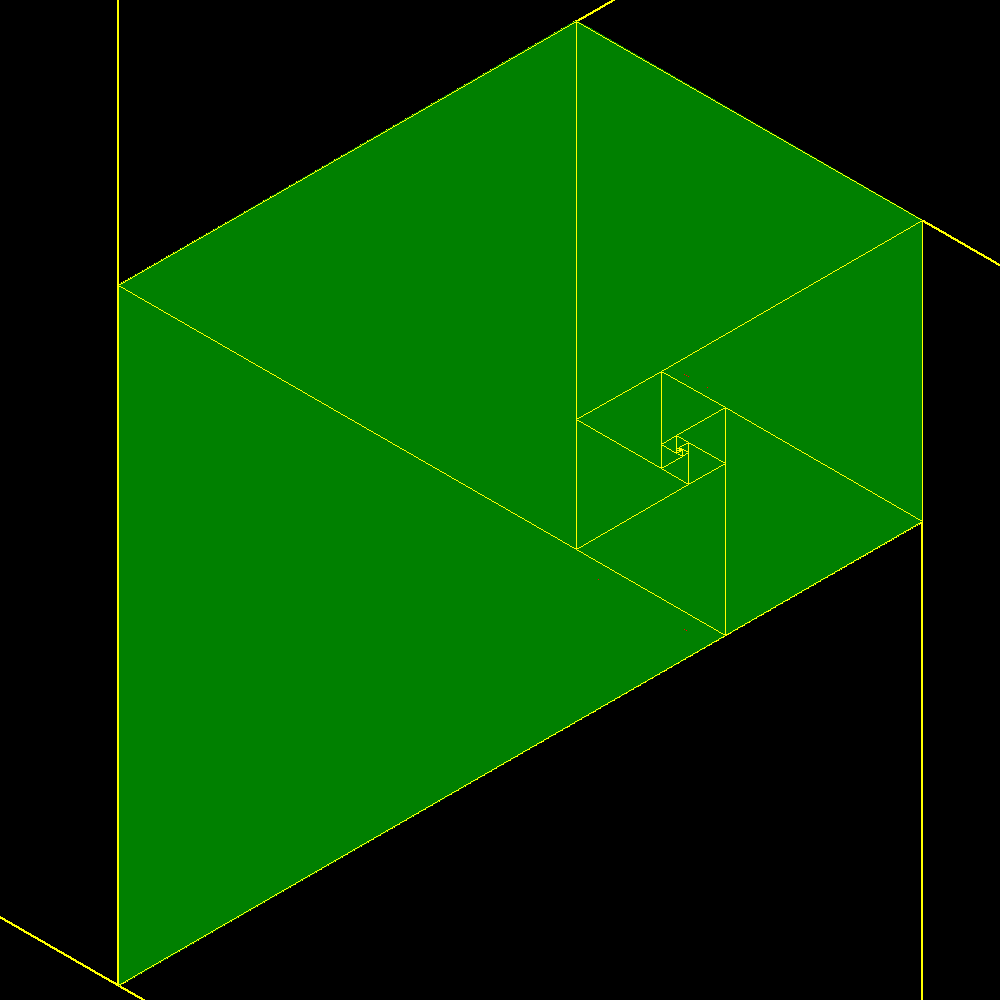
Start of construction of trapezes with equilateral triangles according with the Padovan sequence |
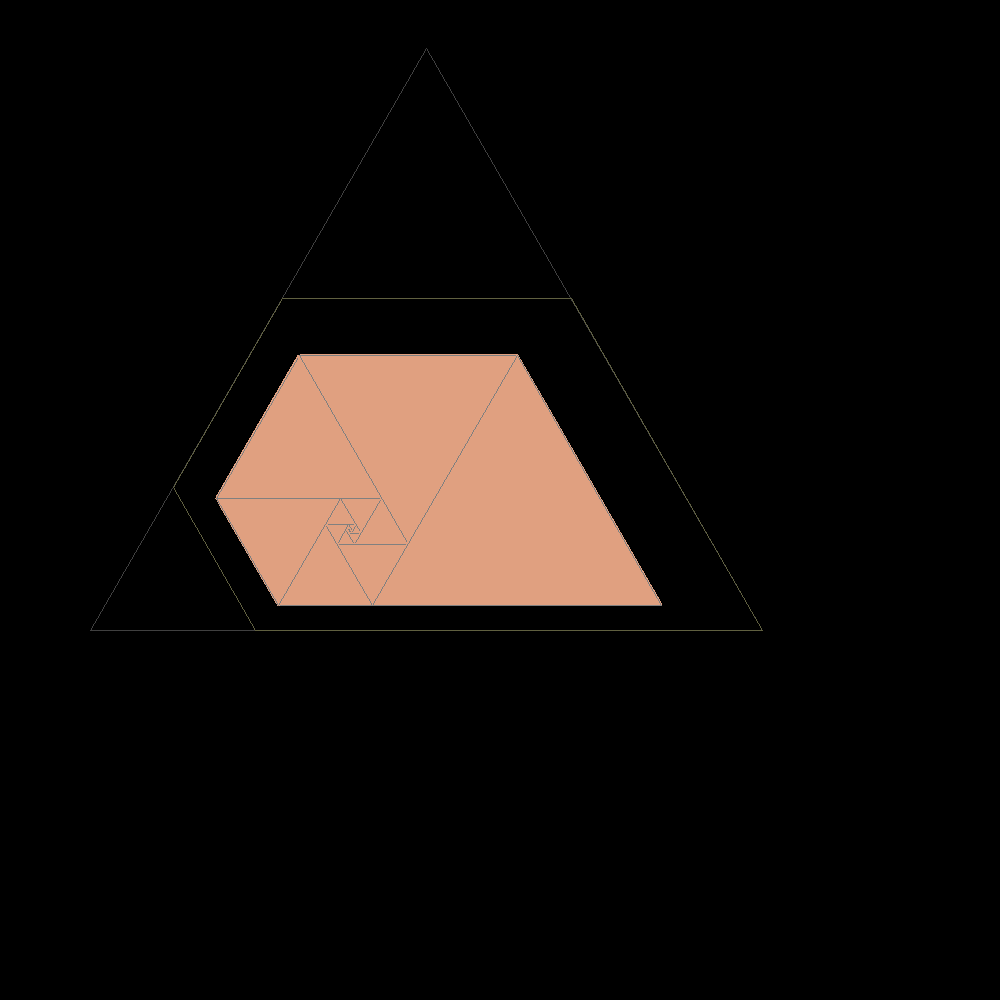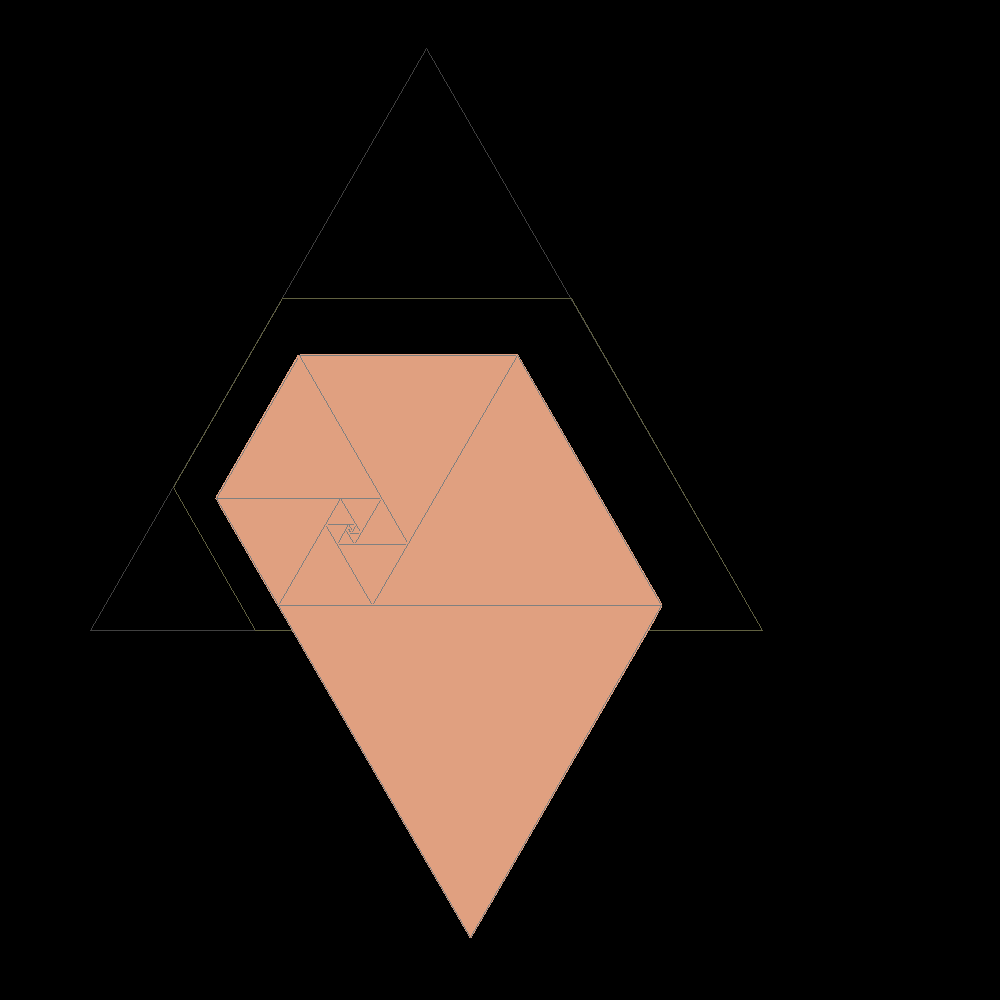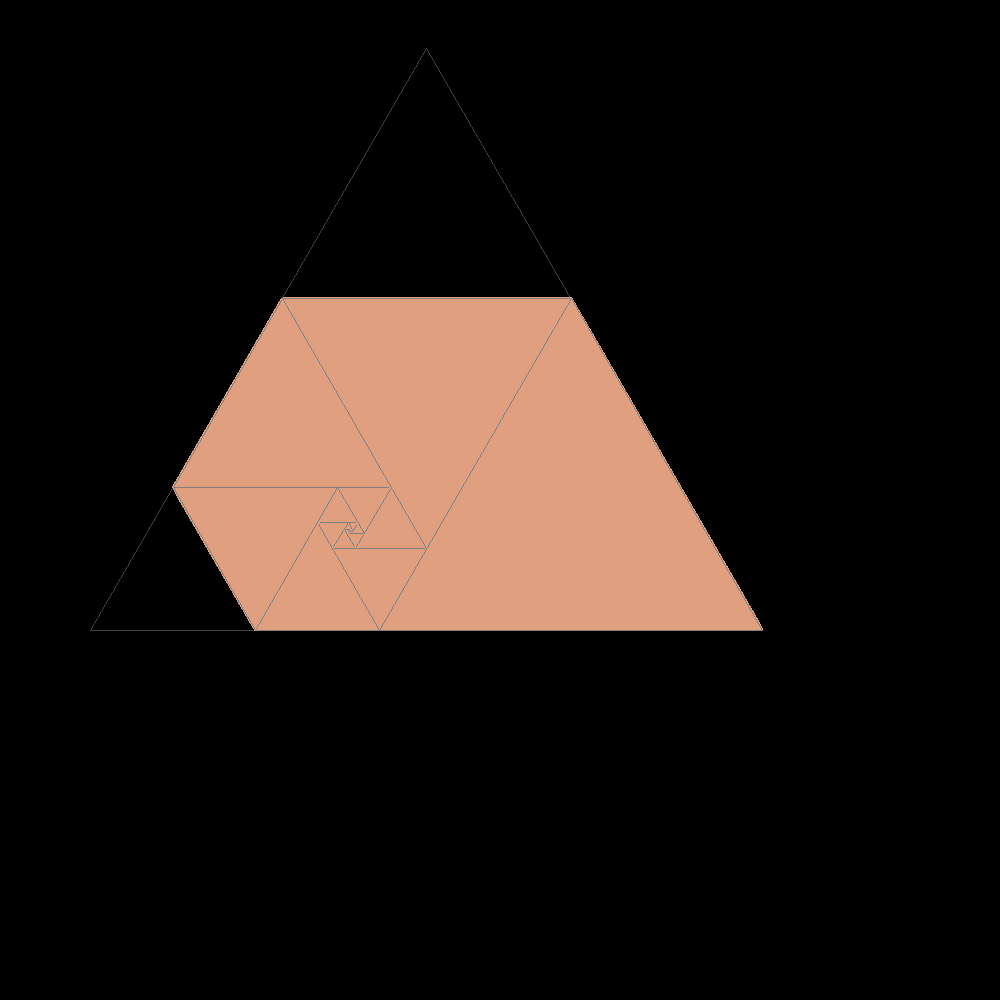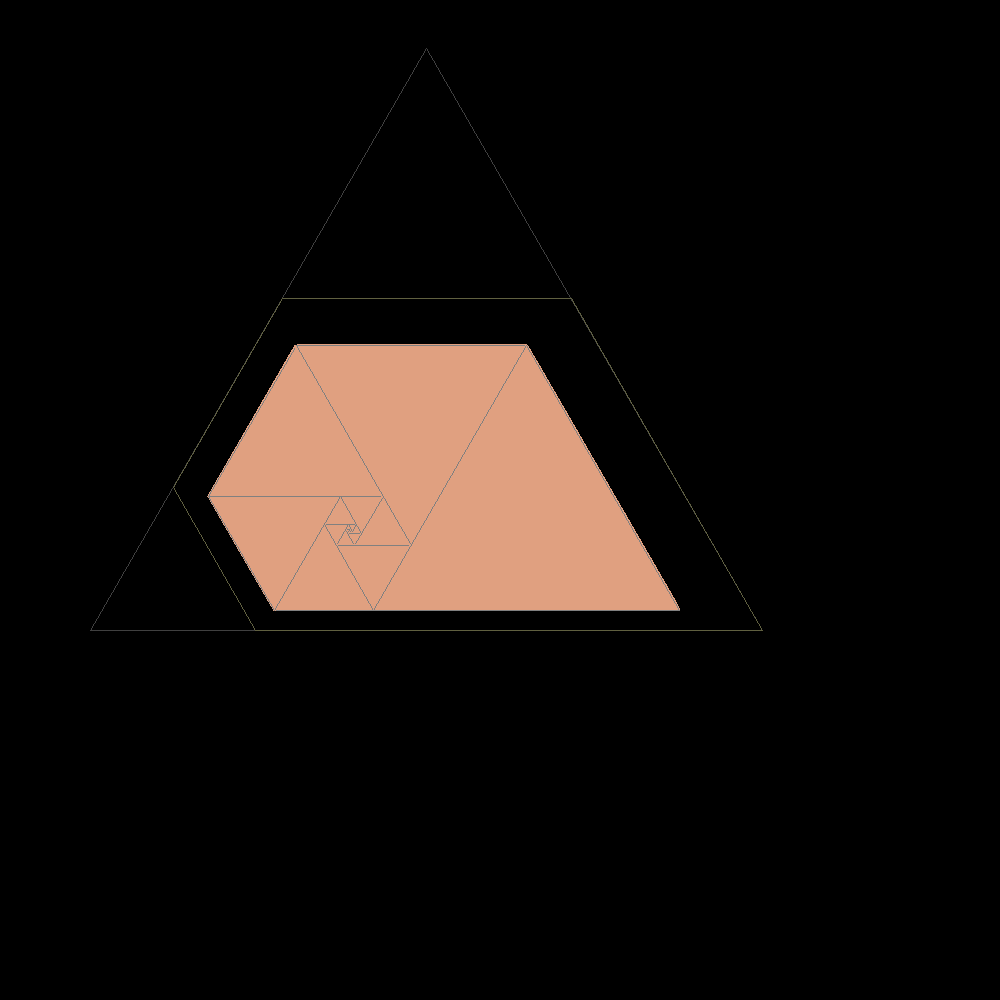 |
|
Shortly after the result is confused with the plastic trapeze to which it tends |
 |
|
Plastic trapeze |
 |
|
packing and unpacking |
