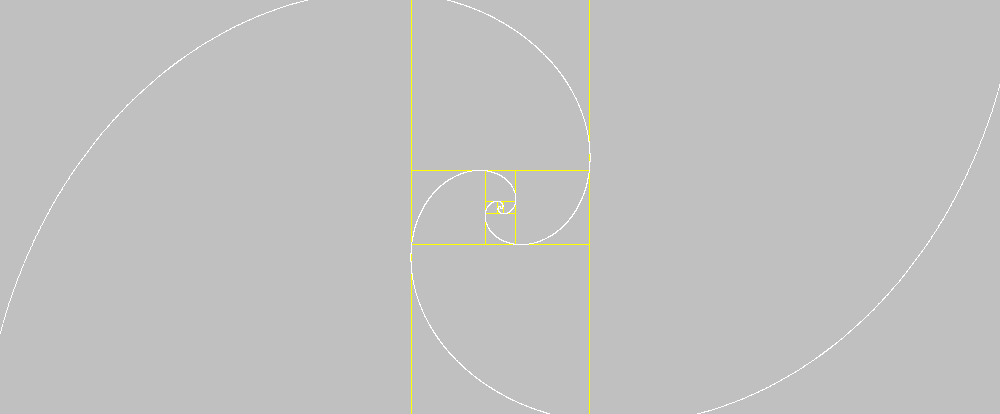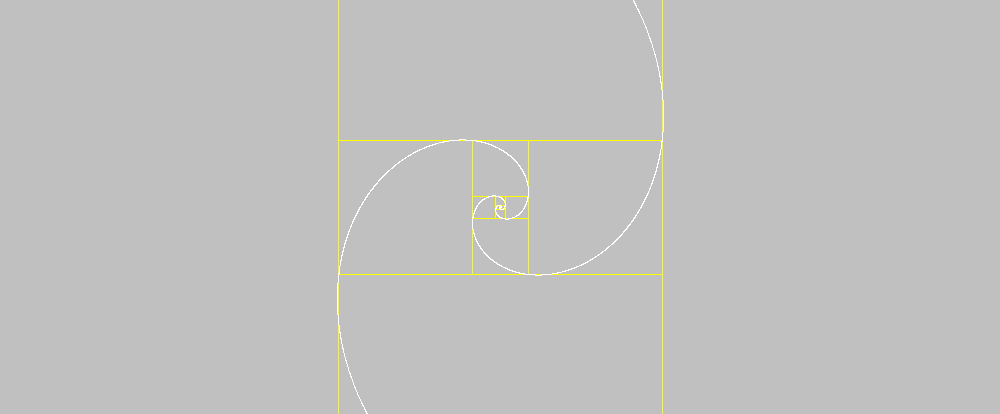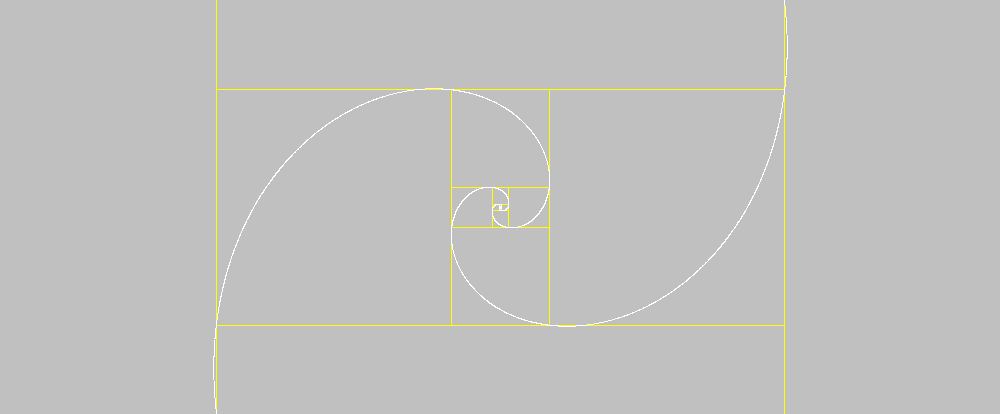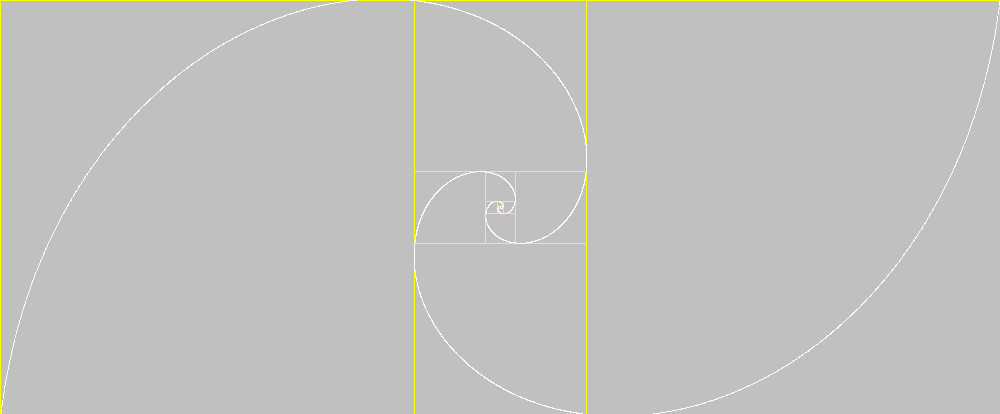
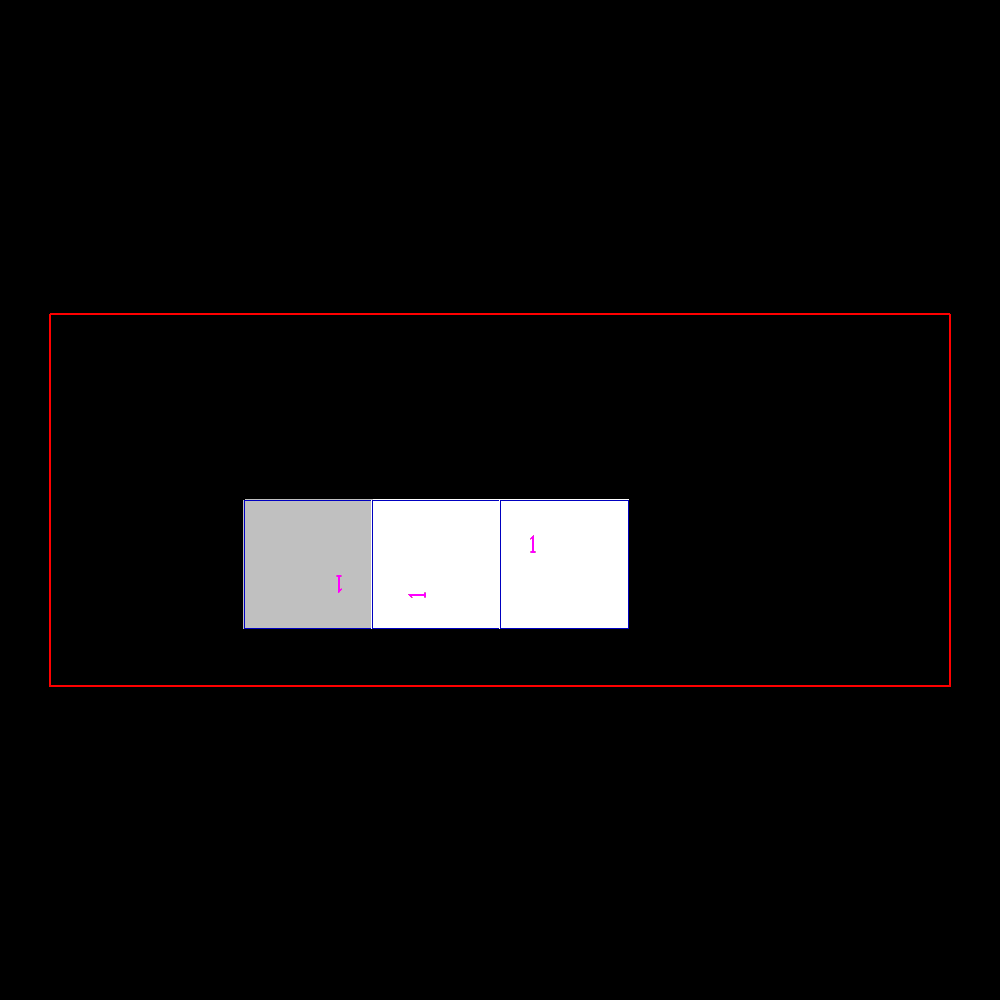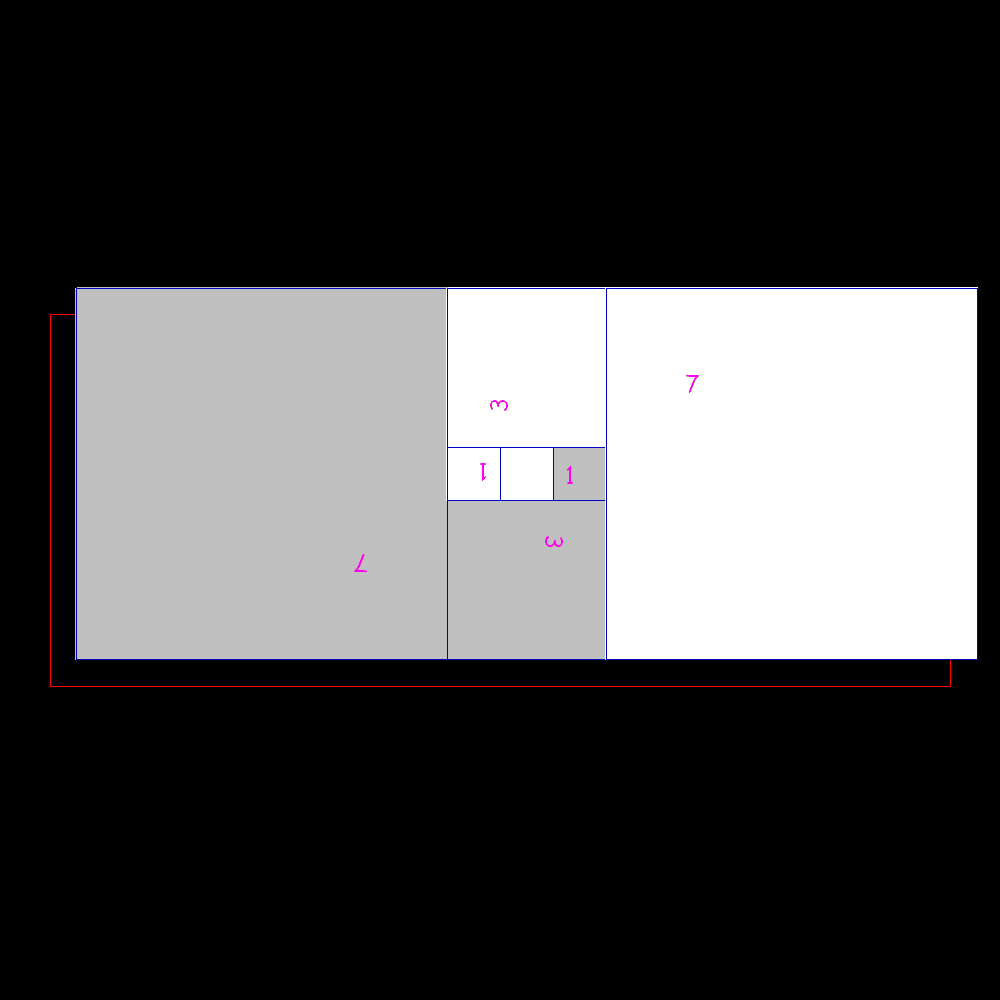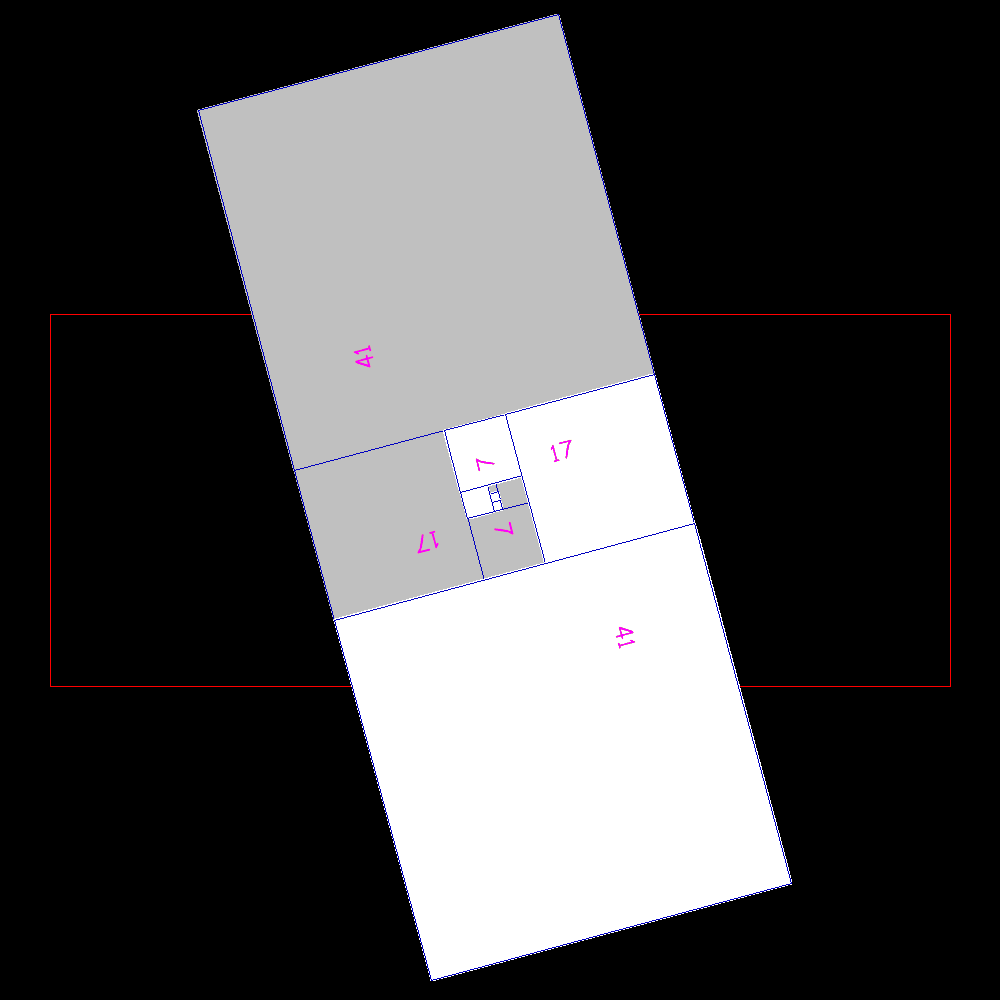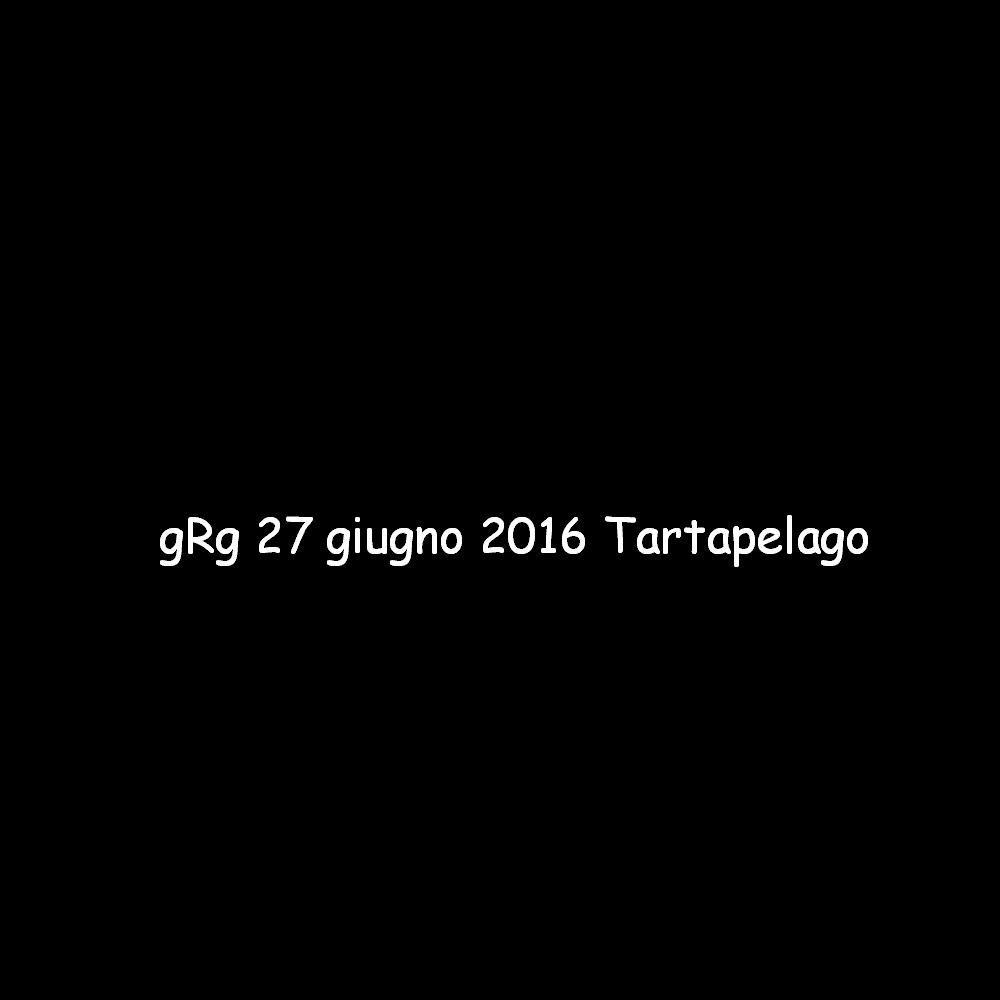
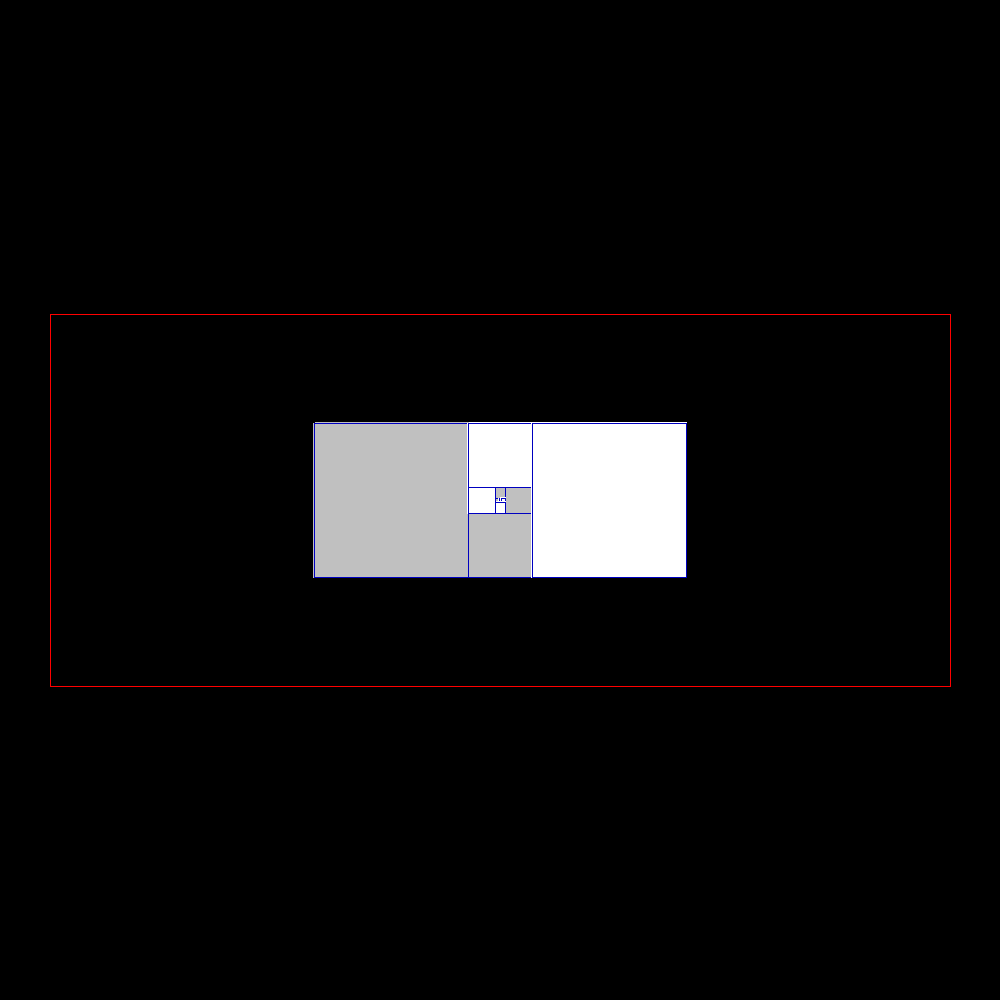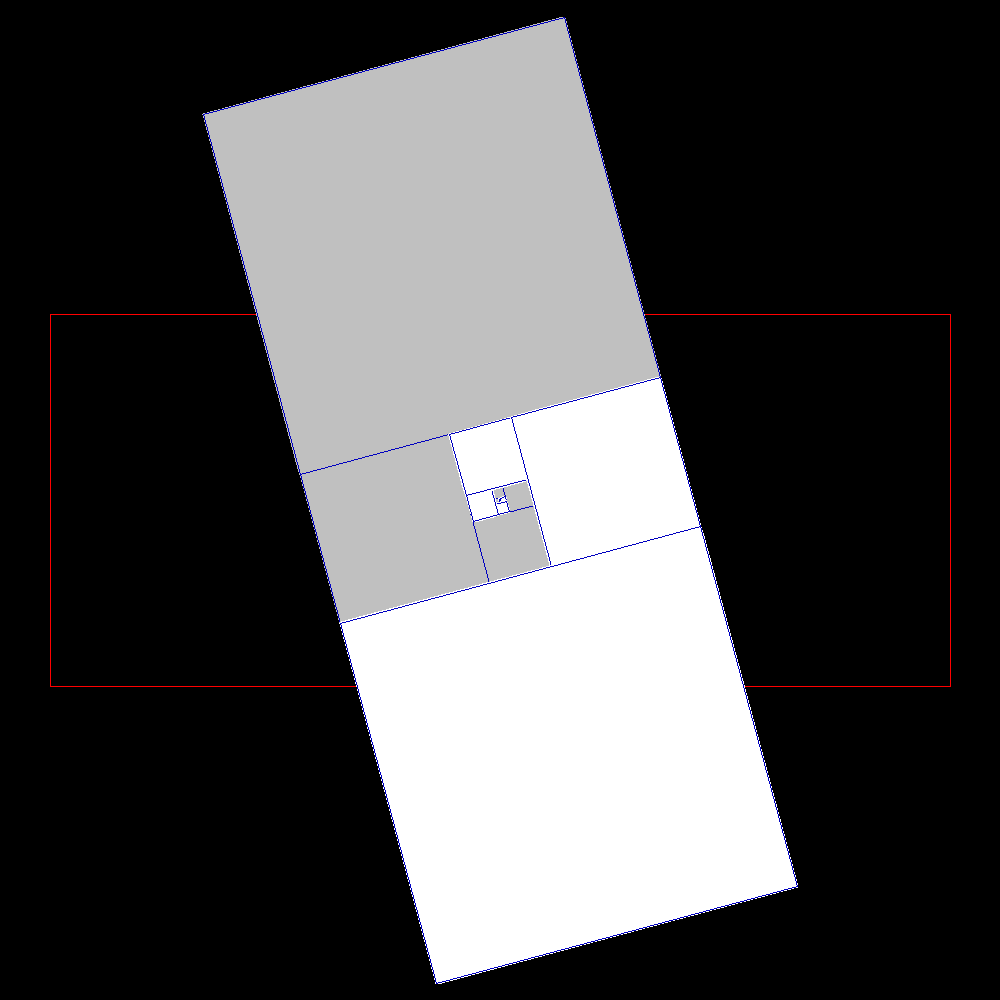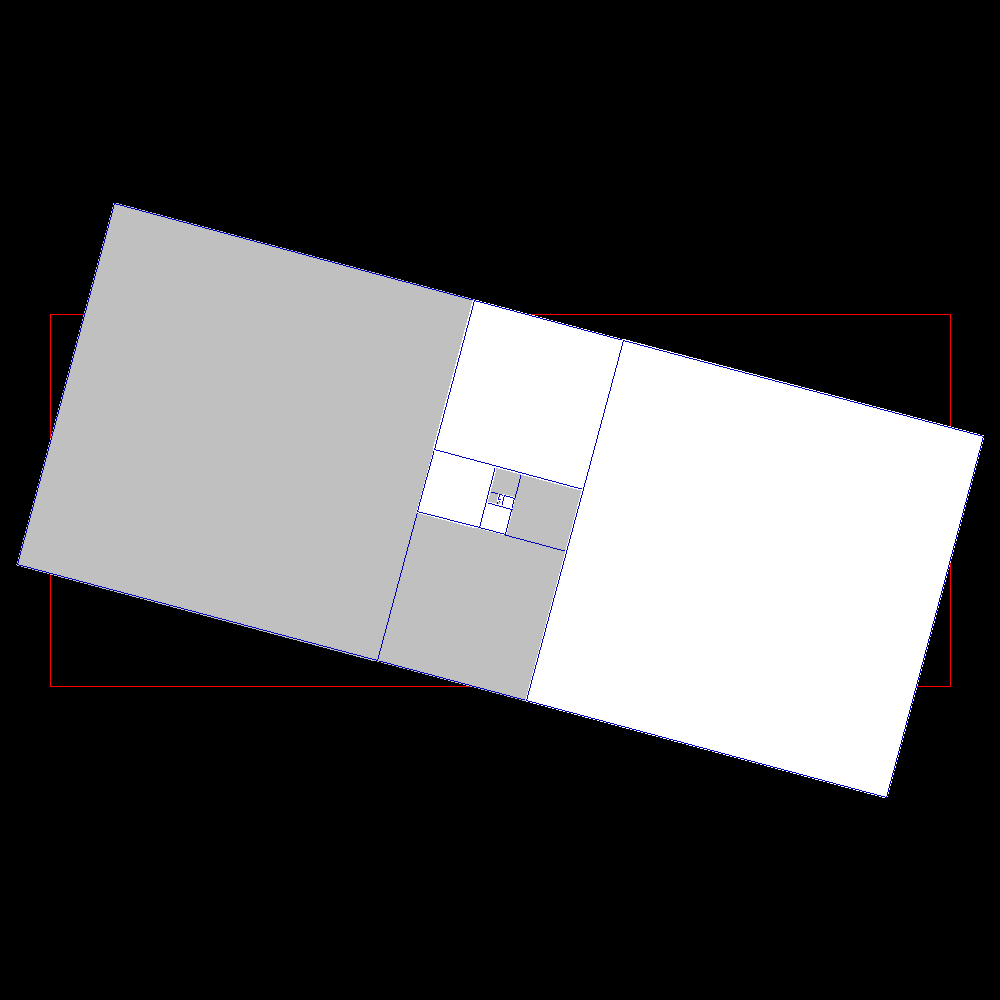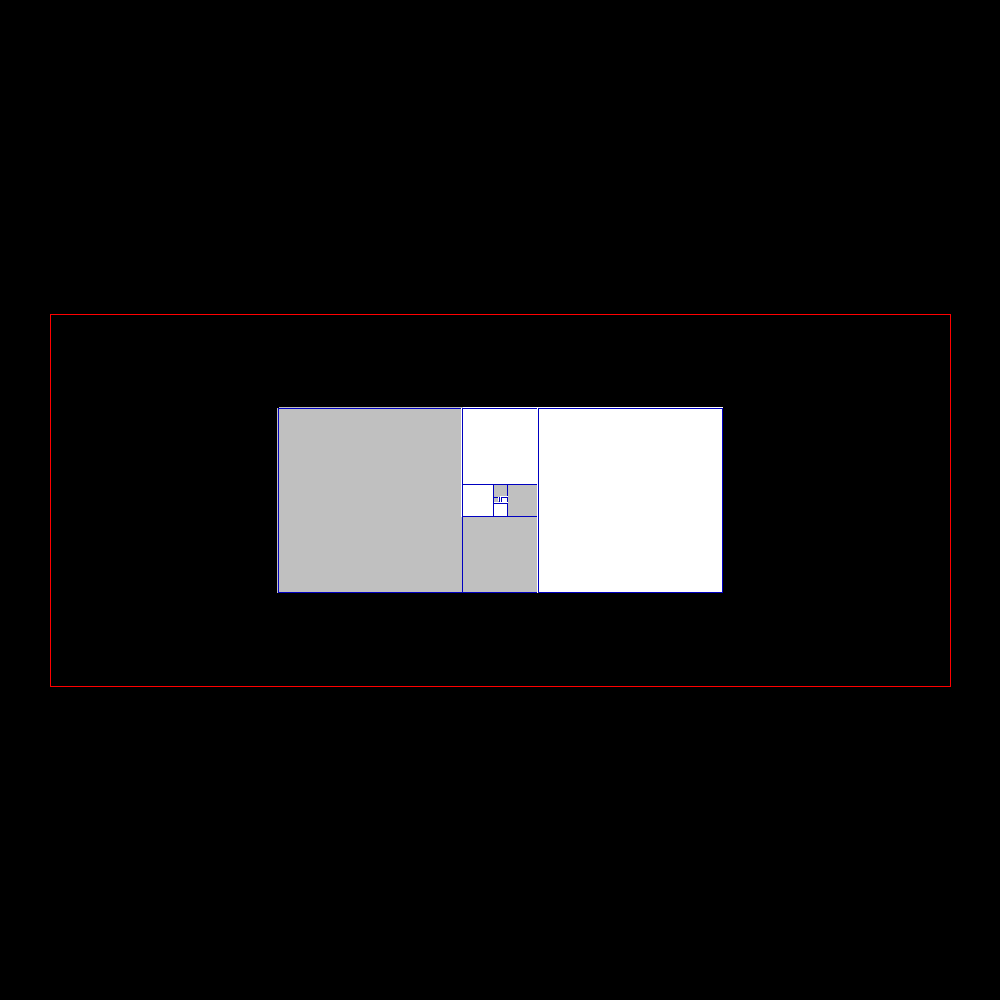
Silver rectangle and its sequence

It can be observed that the side of a square equals the sum between two times the immediately preceding and the one before that.
For that you may tend to silvery rectangle building as squares with the rising edge in the following sequence:

1, 1, 3, 7, 17, 41, 99, 239, 577, 1393, 3363, 8119, 19601, 47321, 114243, 275807,... 
 

Ratio of two consecutive numbers of the sequence tends to the relationship between major and minor side of the silvery rectangle
2.414213562373095...... =1+sqrt(2) 
1/(1+sqrt(2))=sqrt(2)-1=0.414213562373095...

Start of rectangles identified by square building with sides according to the silver sequence

Shortly after the result is confused with the silver  rectangle to which it tends

packing and unpacking