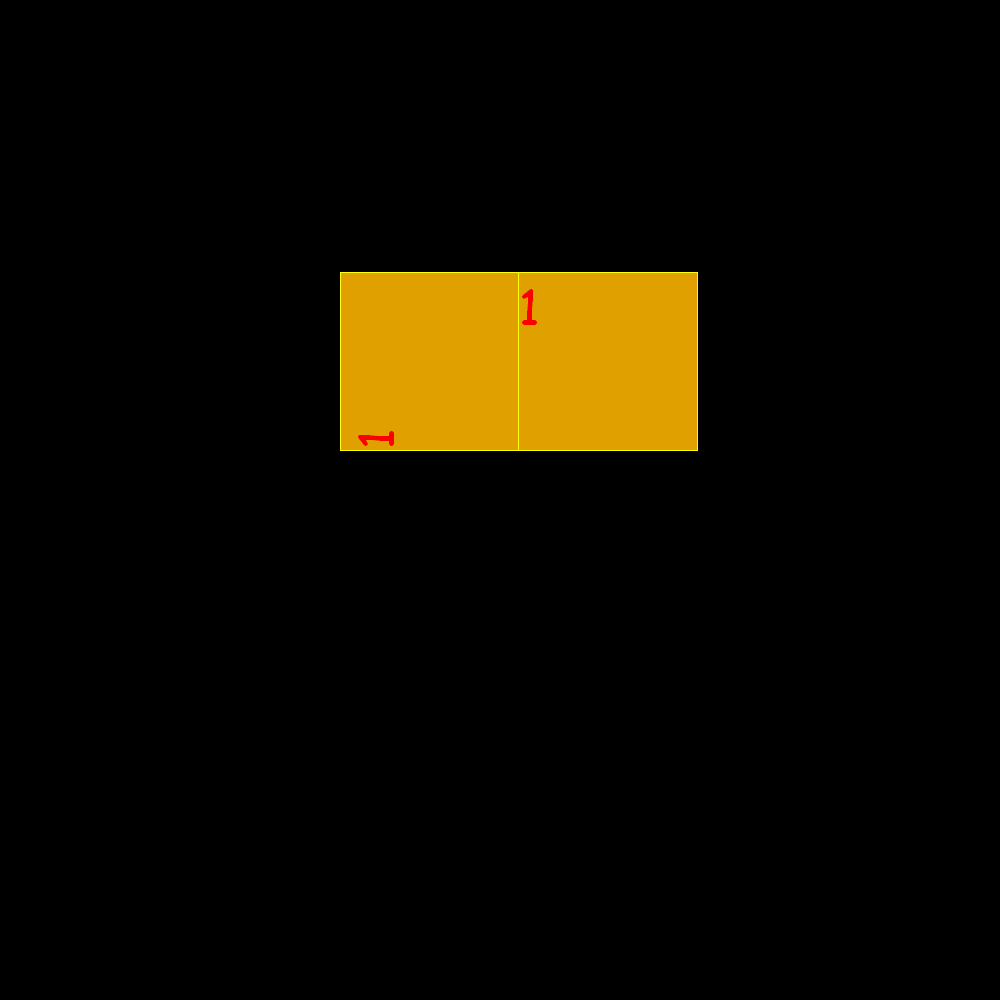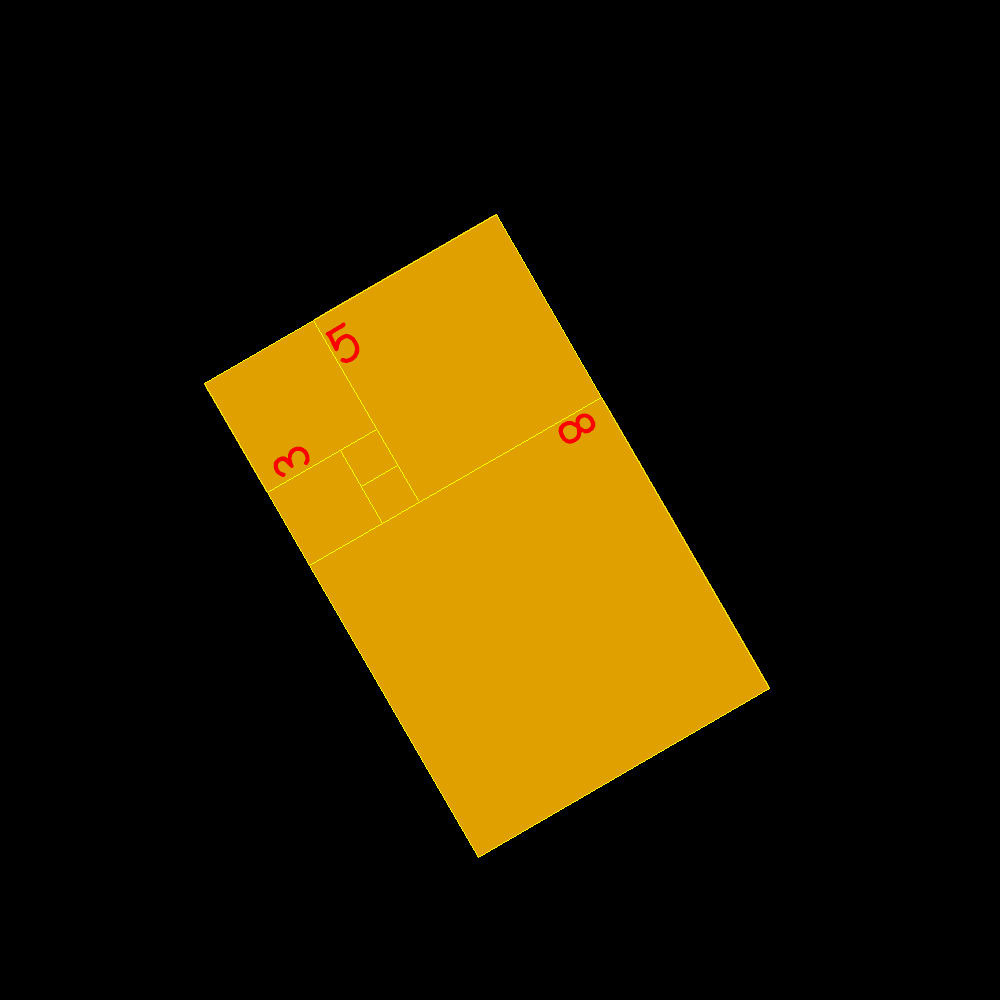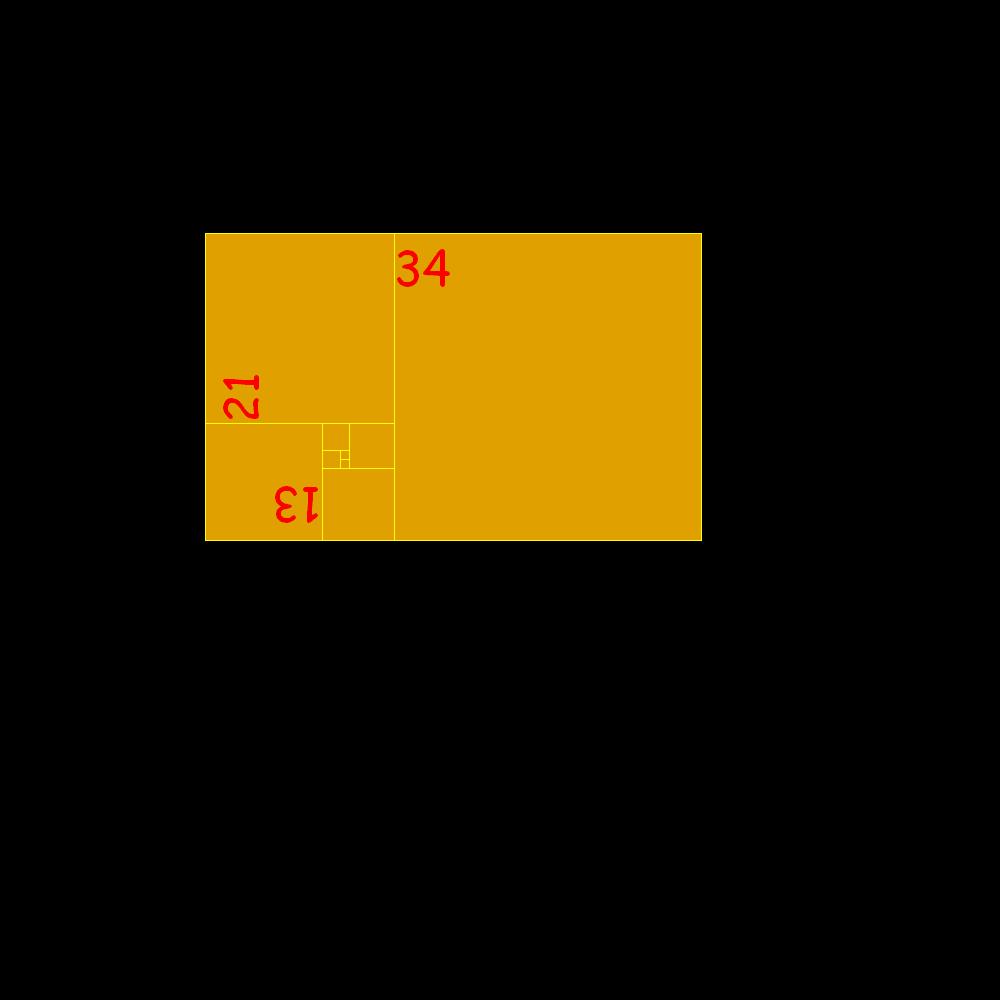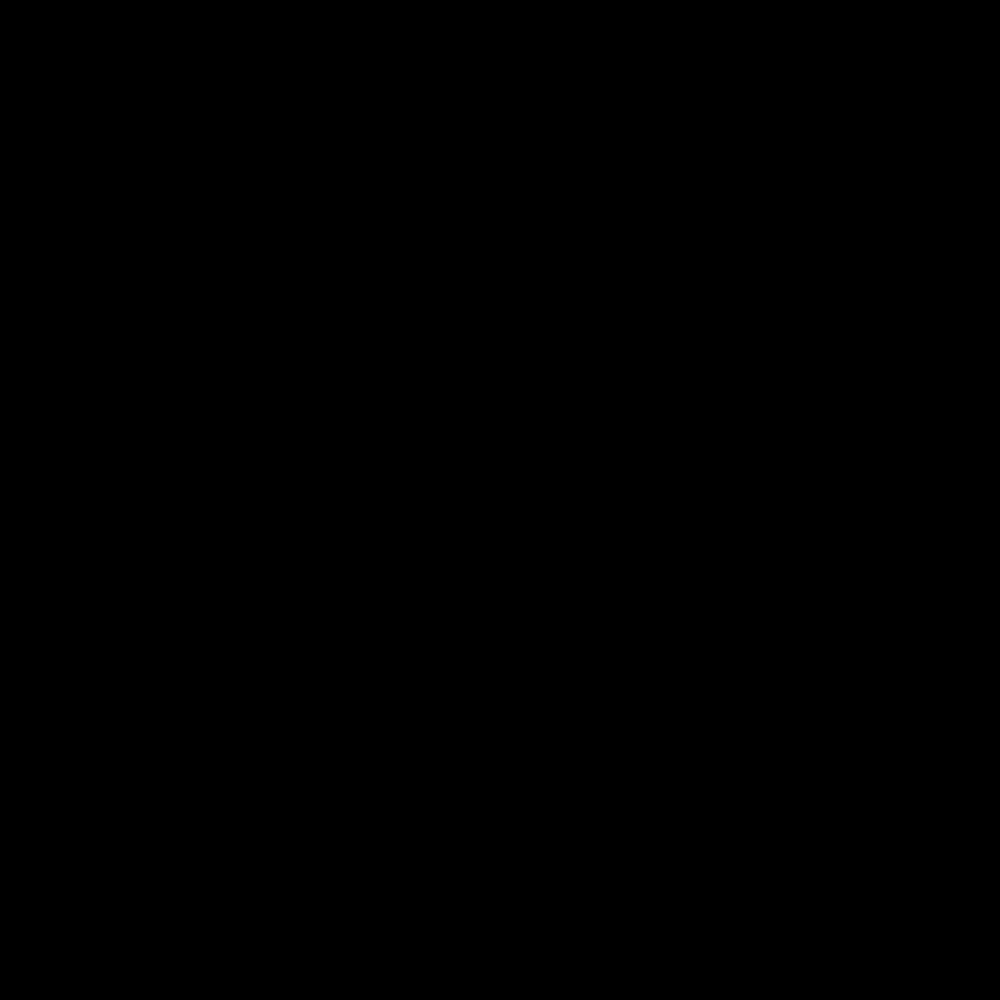
Verso il rettangolo aureo 1/2

Costruendo rettangoli in modo che  il lato di un quadrato uguagli la somma tra i due immediatamente precedenti si tende al rettangolo aureo. Ecco la sequenza dei lati crescenti:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 144,  233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, ...

che sono proprio i famosi numeri con cui Fibonacci contava le successive coppie di conigli

Il rapporto tra due numeri consecutivi della successione tende al rapporto tra lato maggiore e minore del rettangolo aureo:

f =1.6180339887499....       soluzione dell'equazione:
r²-r-1=0

English version
Golden rectangle and Fibonacci sequence