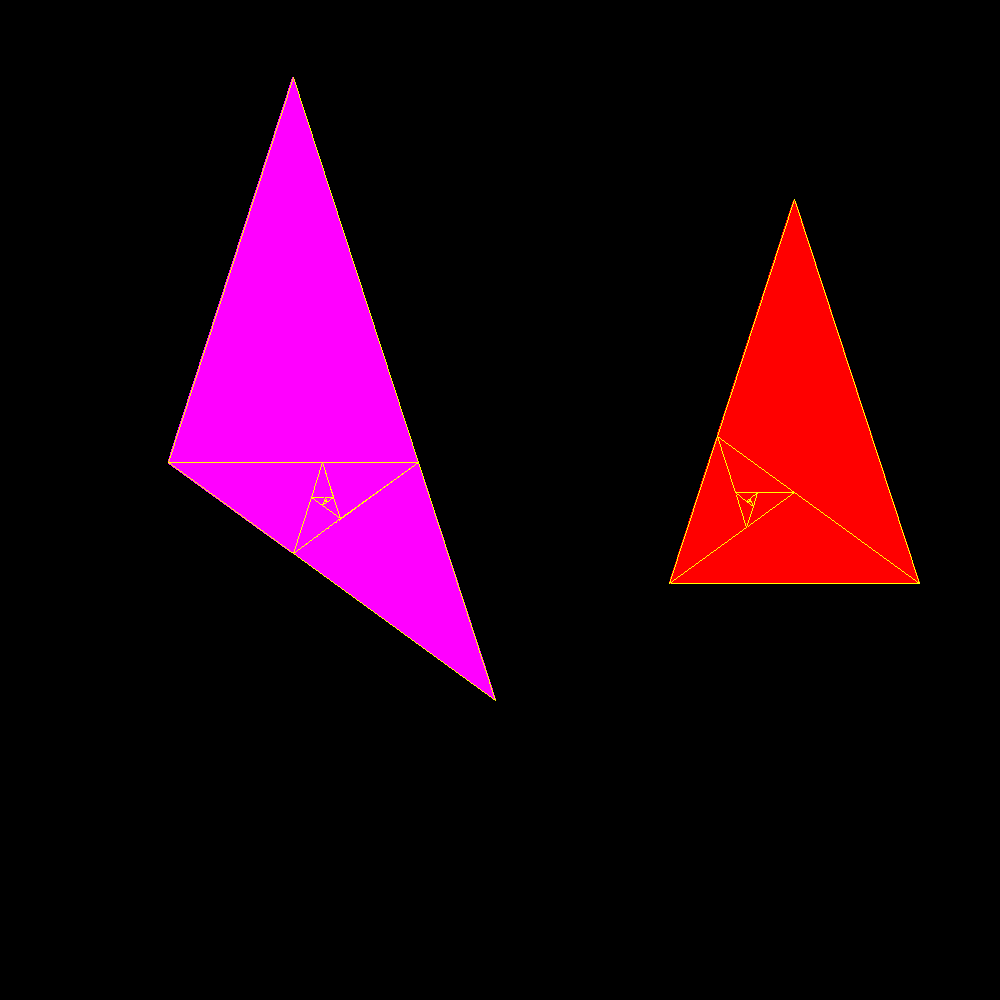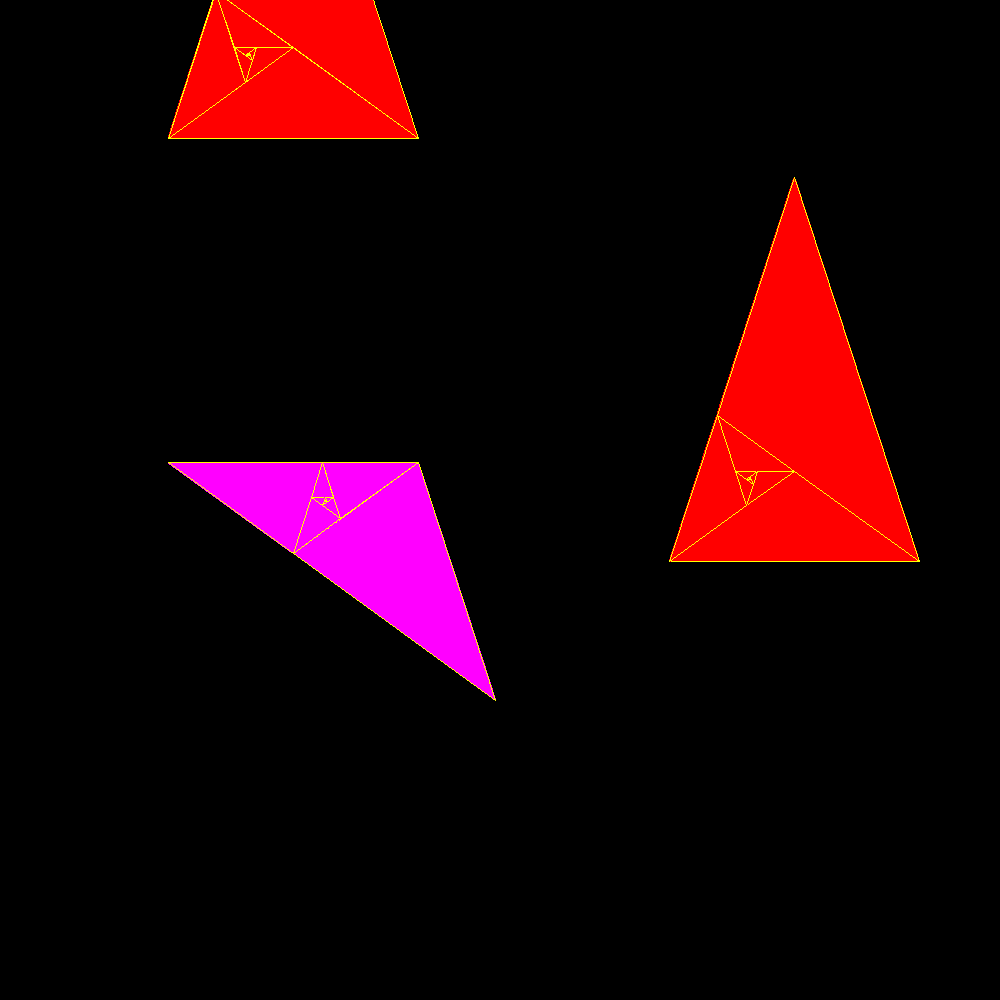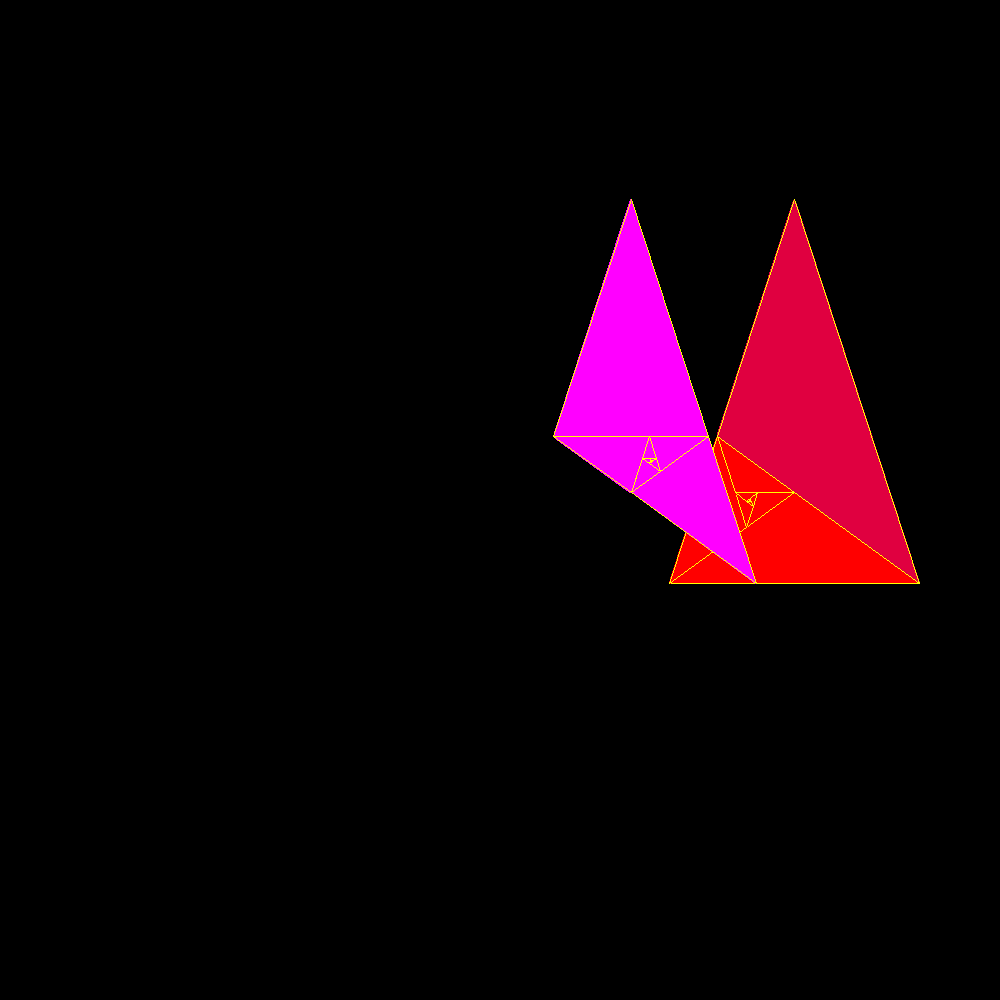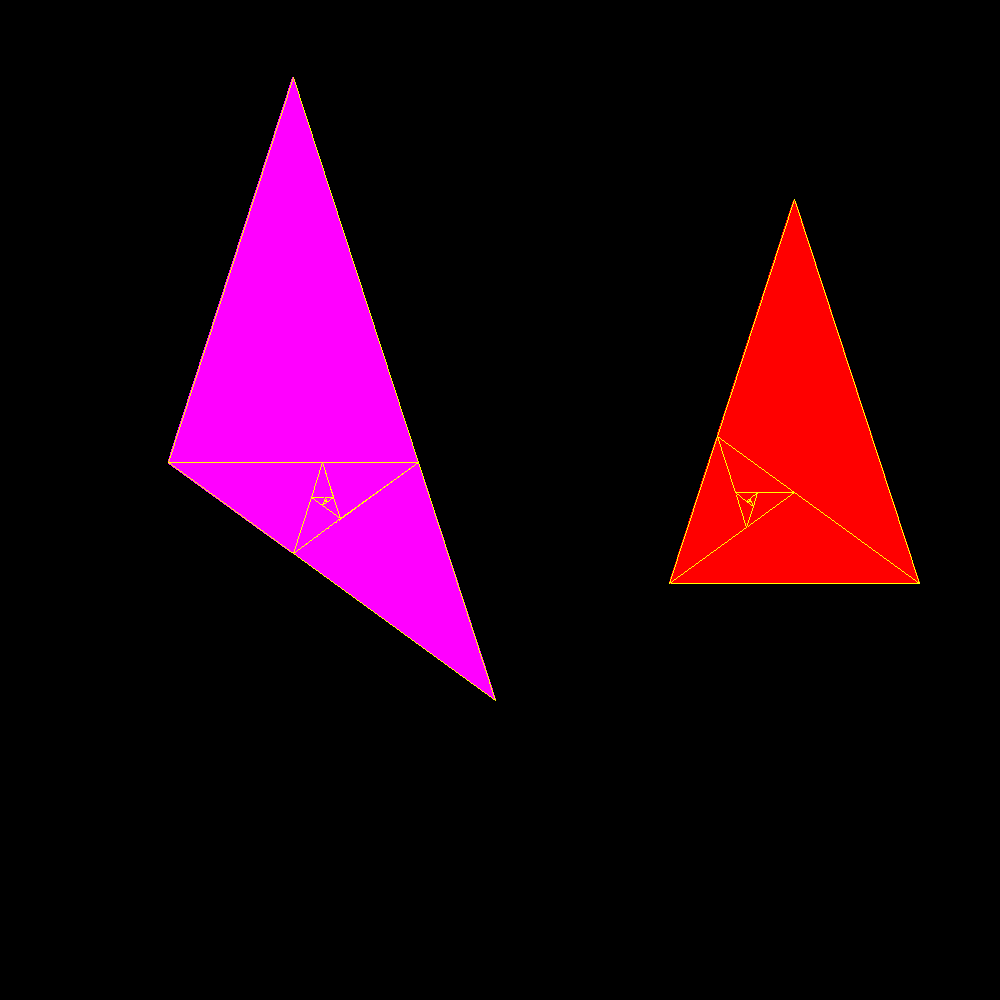|
The extraordinary reciprocity of golden triangles |
|
|
|
According to the definition of Heron of
Alexandria |
| Here are two famous golden triangles. Two isosceles triangles with the different sides in golden ratio, the first without and the second with obtuse angle. Of these is shown clearly their extraordinary reciprocity. The acute is the sum of an infinite series of obtuse as well as the obtuse is the sum of an infinite series of acute. In both cases the sides of the geometric series of triangles decrease in golden ratio. This wonderful property, inevitably, is in sharp contrast with the use as widespread as incorrect and discriminatory to reserve the term golden triangle only the acute and obtuse would simply be the gold gnomon. In fact, at least according to the previous definition of gnomon, one can see that it is true that the golden obtuse is the gnomon dell'acutangolo the reverse is no less true! Much better would then call both acute and obtuse golden triangles or golden of first kind and gold of the second kind. |
 |
|
The first golden triangle |
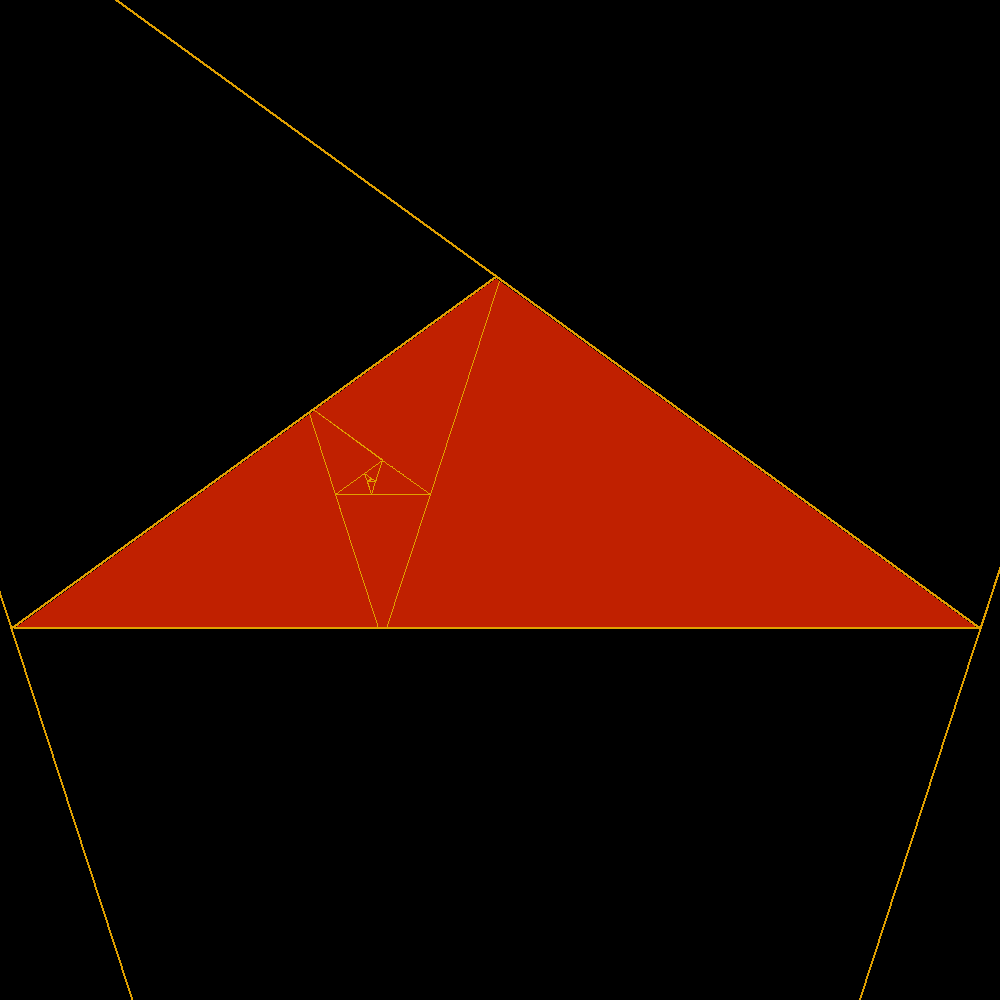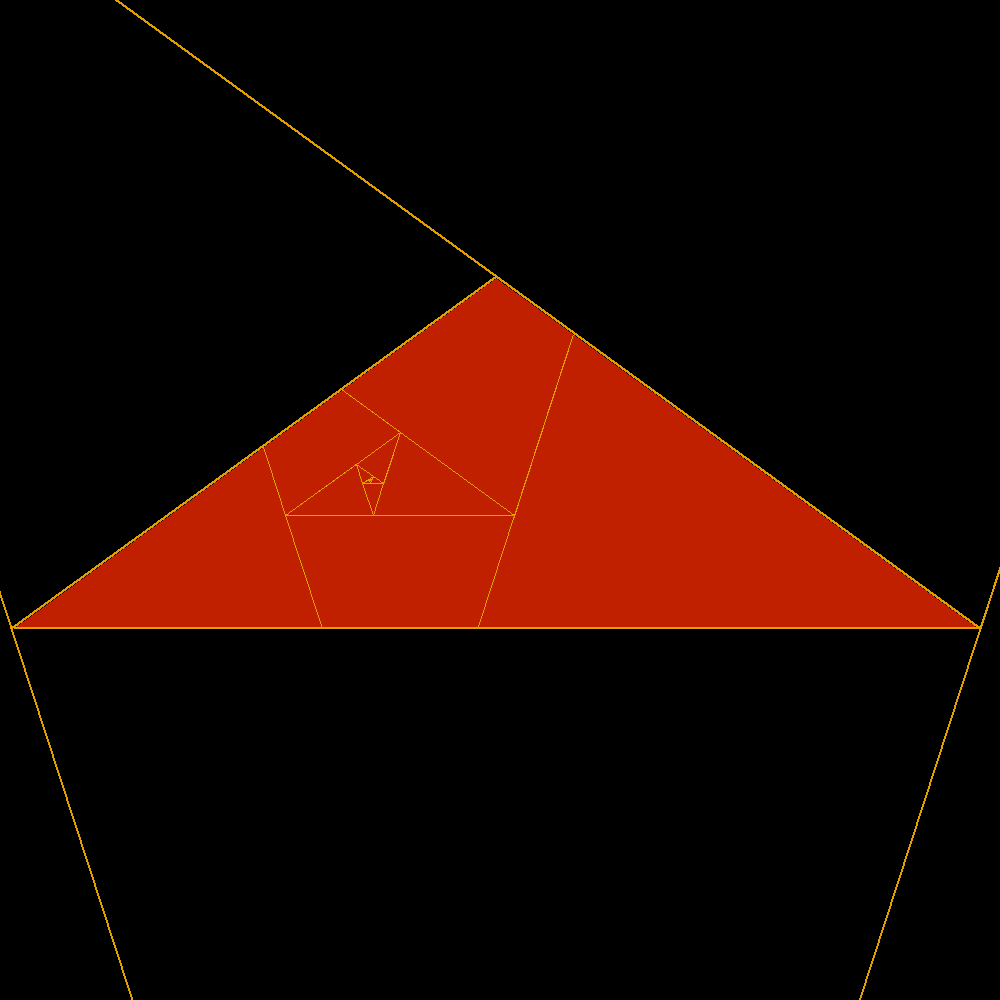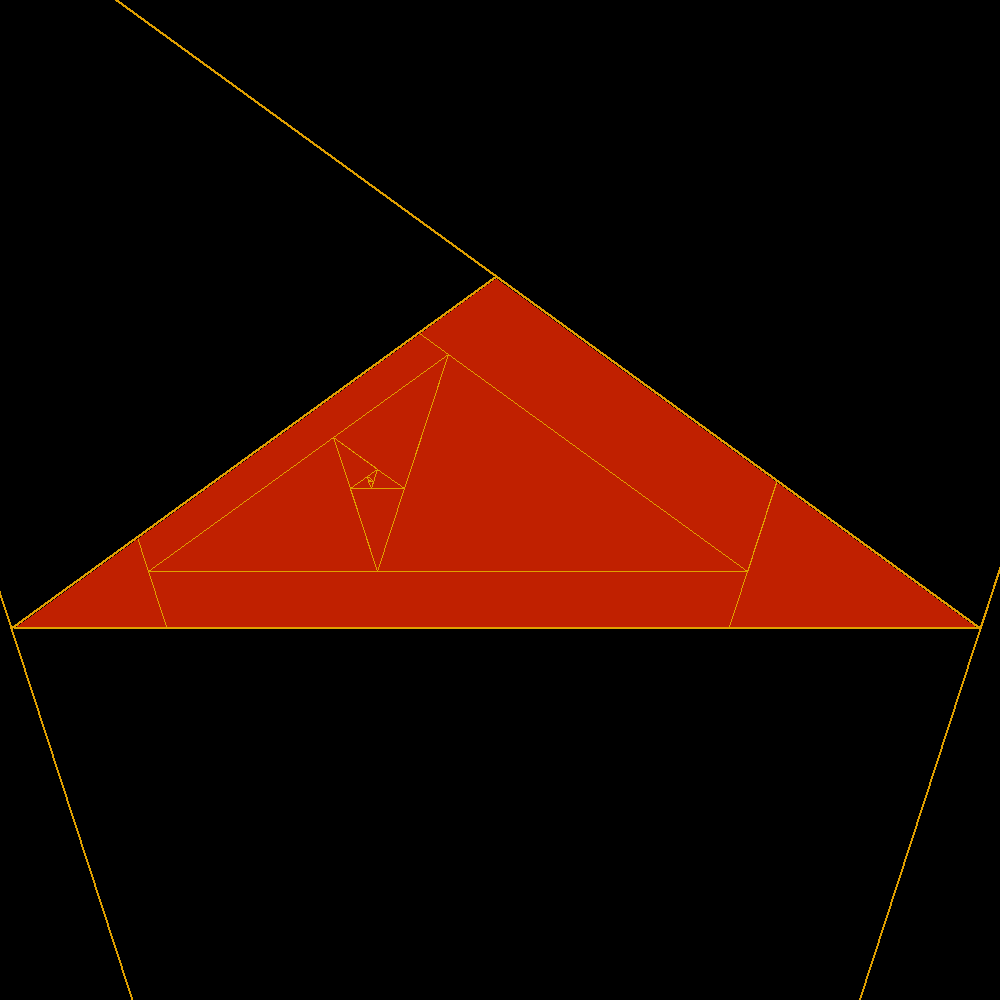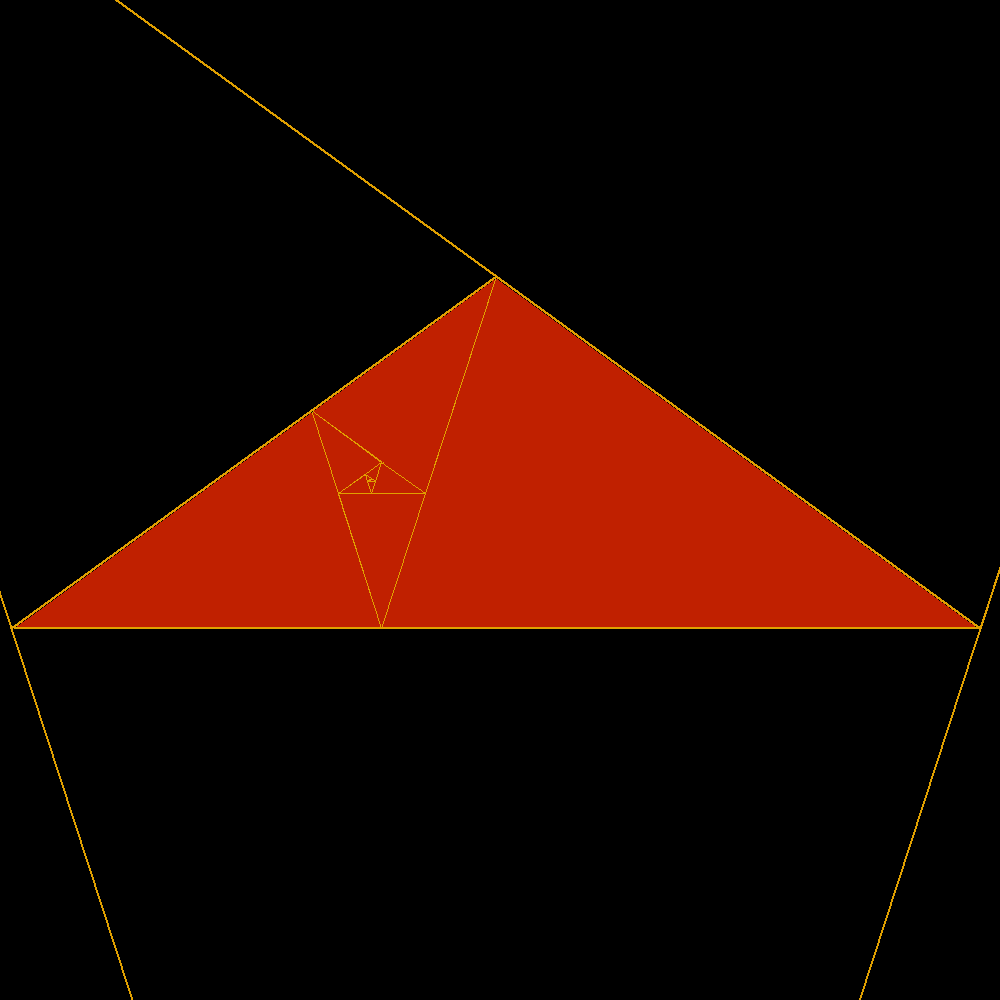 |
|
The second golden triangle |
 |
|
packing and unpacking |
 |
|
packing and unpacking |