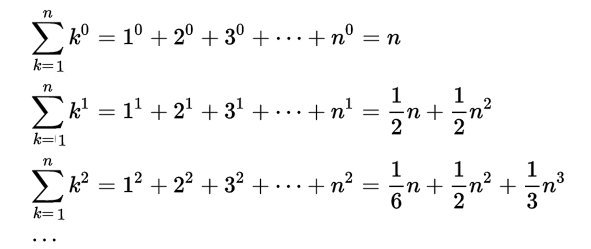
Sui polinomi per il calcolo di somme di potenze di interi successivi e sui numeri di Bernoulli dedotti e dimostrati con il triangolo di Tartaglia
di Giorgio Pietrocola
giorgio.pietrocola[at]gmail.com
ricerca ancora in corso:
Versione del 30.giugno 2017
Indice
1. Il problema della somma di potenze
3.1 Due matrici alternate hanno lo stesso determinante
3.2 Se due matrici sono in relazione di alternanza...
4.La matrice del triangolo di Tartaglia
4.1 Matrici triangolari ritagliate...
5.1 Nota su un identità attribuita a Pascal
7.1 Coefficienti di grado massimo
7.2 Coefficienti dei monomi secondi
7.3 Differenze tra la matrice G e la sua…
7.4 Teoremi sulla ripetizione di zeri
7.5 Numeri di Bernoulli
7.6 I coefficienti dei monomi di …
7.7 Formula diretta per i numeri di Bernoulli
7.8 Formule ricorsive
8. La formula rivelata in “Ars conjectandi”
10.1 funzione generatrice della variante negativa
10.2 funzione generatrice della variante positiva
11. altre relazioni con le matrici considerate
11.2. Fattoriali crescenti e decrescenti
11.3. Altre relazioni notevoli
Sommario
Partendo da un punto di vista diverso dal tradizionale si affronta il problema classico della determinazione dei coefficienti dei polinomi per il calcolo delle somme di potenze di interi successivi. Si dimostra che questi coefficienti possono essere calcolati invertendo una matrice tratta dal triangolo di Tartaglia senza ricorrere ai numeri di Bernoulli. Questi ultimi vengono poi definiti utilizzando le matrici considerate e si cerca, per questa via, di dimostrarne le proprietà, compresa quella rivelata da Jakob Bernoulli nel suo “Ars conjectandi”. Infine si evidenziano relazioni, ancora da approfondire, di queste matrici con elementi correlati come i polinomi di Bernoulli e i numeri di Stirling.
1.Il problema della somma di potenze.
Il problema consiste nell’ottenere la somma di un certo numero n di potenze di interi successivi elevati ad un certo esponente intero m mediante un polinomio che ne faciliti il calcolo. Con m=0 il problema è banale perché gli n addendi valgono tutti 1 e la somma è quindi n (polinomio di primo grado). Con m=1 si tratta di trovare la somma dei primi n numeri naturali, Si può risolvere rapidamente pensando di raddoppiare somma e risultato, Associando opportunamente addendi crescenti e decrescenti delle due somme si ottiene n volte 1+n, dividendo per due come quando si calcola l’area di un triangolo si arriva al polinomio di secondo grado cercato. Nei casi successivi esiste sempre un polinomio di grado via via crescente ma mentre alcuni coefficienti dei monomi appaiono facilmente prevedibili altri sembrano succedersi in modo piuttosto caotico.
Ecco a titolo di esempio i primi casi:
Questi primi risultati possono essere efficacemente riassunti utilizzando il prodotto righe per colonne tra matrici:
Se invece di partire da 1 si parte da zero per fare n addendi ci si ferma a n-1 per cui le somme possono anche essere espresse così:
Che si può anche scrivere:
Indicheremo, al variare degli indici che ne indicano le dimensioni, le matrici dei polinomi in questo modo:
2. Introduzione storica
Il fascino di questo problema ha attratto matematici sin dall’antichità. Già Nicomaco di Gerasa (circa 60-120) dimostrò un sorprendente teorema che ora porta il suo nome:
ossia, in forma compatta:
Nel 1631 il tedesco Jhoann Faulhaber (1580-1635) pubblica su Accademia Algebrae un suo studio dove presenta molti polinomi che risolvono il problema in casi particolari. Per esempio proseguendo la strada di Nicomaco trova per gli esponenti dispari:
D.Knuth, Tratto dalllo studio di D.Knuth , Johan Faulhaber and sum of power ,Internet Archive, 1992 |
Ulteriori progressi si hanno con lo svizzero Jakob Bernoulli (1654-1705). Nel 1713 viene pubblicato postumo il suo Ars Conjectandi di cui riportiamo la pagina fondamentale. Qui troviamo per la prima volta una legge generale, espressa in funzione di numeri particolari presi per la prima volta in considerazione, per trovare i polinomi che calcolano le varie somme di potenze al crescere dell’esponente.
Come si vede il generico polinomio relativo alla potenza c si costruisce agevolmente per quanto riguarda i due monomi di grado più alto poi però per gli altri coefficienti il calcolo diventa via via più laborioso ma soprattutto dipende da numeri molto particolari indicati dall’autore in maiuscolo con le prime lettere dell’alfabeto. Sono i misteriosi numeri che i matematici successivi chiamarono numeri di Bernoulli. Il contenuto della pagina mostrata sarà ripreso ed espresso in notazione attuale al paragrafo 8. Qui mettiamo in evidenza un errore, probabilmente di stampa, in uno dei coefficienti del polinomio di decimo grado. Ecco riportati in una matrice i valori corretti: |
La legge generale scoperta da Bernoulli che ricava in modo mirabile i coefficienti dei polinomi a partire dai suoi particolari numeri sarà dimostrata solo nel 1834 da Carl Gustav Jacobi[1](1804-1851) utilizzando una via analitica. Sulla stessa strada il suo allievo Bernhard Riemann (1826-1846) introdurrà l’importantissima funzione zeta pure connessa con i numeri di Bernoulli. Scoperta l’importanza di questa sequenza infinita di numeri si pose il problema del loro calcolo. La matematica inglese Ada Byron (1815,1852), contessa di Lovelace dopo il matrimonio contratto all’età di 20 anni, e figlia del noto poeta Lord Byron con cui non ebbe mai alcuna relazione essendo stata, per l’abbandono del padre, allevata solo dalla madre, nel 1843 pubblica un commento all’opera del connazionale Charles Baggage (1791-1871) ideatore di una macchina meccanica programmabile che non potè essere realizzata per motivi economici. Tra le sue note vi era il primo programma informatico della storia, la descrizione di un algoritmo proprio per calcolare i numeri di Bernoulli con la macchina analitica di Babbage.
Oggi dopo quasi due secoli, con i moderni strumenti di calcolo, ci si è spinti molto avanti nel calcolo di questi numeri tanto che in rete [2] si può trovare
3. La relazione di alternanza e le sue proprietà
Nei paragrafi 3 e 4 daremo alcune nozioni propedeutiche all’approccio scelto per affrontare il problema.
Diremo che due matrici quadrate invertibili delle stesse dimensioni X e Y sono in relazione di alternanza se i corrispondenti elementi sono nella seguente relazione:
evidenzieremo questa relazione scrivendo:
Diremo anche che la matrice X è uguale all’alternata di Y e viceversa data la commutatività della relazione.
Per le nostre dimostrazioni è necessario tener presenti i seguenti teoremi:
3.1 Due matrici alternate hanno lo stesso determinante
Infatti se si considera il determinante di una matrice di ordine n come somma di n! addendi ognuno composto da n fattori con gli indici di riga fissi e quelli di colonna permutati in tutti i modi possibili si vede che questi addendi rimangono invariati se si passa alla matrice alternata. Infatti così cambiano di segno solo quei fattori che hanno dispari la somma degli indici. Questi cambiamenti però in ogni addendo dovranno essere in numero pari perché se fossero dispari anche la somma complessiva degli indici di riga e di colonna dell’intero addendo composto di n fattori dovrebbe essere dispari mentre, essendo la doppia somma 1+2+...+n vale n(n+1) che è pari. Cambiando di segno, quindi, necessariamente, solo un numero pari di fattori il prodotto e quindi il relativo addendo non varia e neppure gli n! addendi la cui somma dà il determinante.
3.2 Se due matrici sono in relazione di alternanza anche le loro inverse sono nella stessa relazione
Ciò si ricava facilmente dal precedente teorema tenendo conto che la matrice inversa è l’alternata della trasposta di particolari determinanti che rimangono invariati.
4.La matrice del triangolo di Tartaglia e le sue matrici parziali.
Sviluppando le potenze x+1 si ottengono i seguenti polinomi:
Che possiamo anche scrivere come prodotto di matrici:
Si osservi che la moltiplicazione trasforma la base del vettore di potenze aumentandola di un’ unità. Da questa osservazione si deduce che le potenze successive della matrice quadrata forniscono i coefficienti degli sviluppi delle potenze di x+2, x+3 e così via. Allo stesso modo l’inversa di Tn e le sue potenze sottrarranno unità alla base. Infatti:
che si può anche esprimere come:
Indichiamo queste matrici quadrate nel seguente modo
Dato che i loro effetti moltiplicativi si annullano, infatti una aggiunge e l’altra sottrae un’unità alla base del vettore di potenze, le due matrici sono una inversa dell’altra. Inoltre sono anche in relazione di alternanza.
4.1 Matrici triangolari “ritagliate” dal triangolo di Tartaglia
Ecco come indicheremo matrici private del primo elemento di ogni riga:
Ecco come indicheremo matrici private dell’ultimo elemento di ogni riga:
Notare che quest’ultima matrice a segni alterni ha valori opposti rispetto ai corrispondenti valori nella matrice a segni alterni completa.
5. Teorema 1A
Si dimostra che i coefficienti dei polinomi per il calcolo della somma di n potenze di interi successivi si possono ottenere invertendo una matrice triangolare a segni alterni ricavabile dal triangolo di Tartaglia eliminando l’ultimo elemento di ogni riga. |
Gli elementi di questa matrice possono essere definiti nel seguente modo:
risulta quindi una matrice triangolare in cui compare il triangolo di Tartaglia, a segni alternati, privato dell’ultimo elemento di ogni riga. La sua diagonale principale risulta perciò formata dalla successione degli interi positivi il cui prodotto (m!) ne dà il determinante .
Si ha:
Nei primi due passaggi si è applicata la proprietà distributiva. Nel terzo,quando si moltiplica la matrice quadrata per il vettore di potenze si ottiene:
Dunque si è dimostrato che:
|
Moltiplicando i due membri a sinistra per l'inversa si ottiene:
E’ dimostrato quindi questo teorema
che fornisce i famosi polinomi per il calcolo della somma di potenze di interi successivi.
Esempio con m=11
E applicando il teorema dimostrato:
Si può notare, nella prima colonna della matrice quadrata, la comparsa degli originali numeri di Bernoulli.
Esprimendo questa uguaglianza in forma equivalente otteniamo proprio i polinomi presentati nel libro di Bernoulli:
5.1 Nota su un’identità attribuita a Pascal
Se invece della matrice a segni alternati si usa Am procedendo come visto nel precedente teorema si ottiene:
Ponendo :
possiamo confrontare l’identità di Pascal[3] con quella fondamentale nel teorema 1A:
6.Teorema 1B
Si dimostra che i coefficienti dei polinomi per il calcolo della somma di n-1 potenze di interi successivi si possono ottenere invertendo una matrice triangolare ricavabile dal triangolo di Tartaglia eliminando l’ultimo elemento di ogni riga. |
Prendiamo in considerazione una matrice quadrata, come la precedente ma a segni alternati, di m righe e m colonne così definita:
Questa risulta essere una matrice triangolare in cui compare il triangolo di Tartaglia privato dell’ultimo elemento di ogni riga. La sua diagonale principale é formata dalla successione degli interi positivi il cui prodotto (m!) ne dà il determinante.
Si ha
Nei primi due passaggi si è applicata la proprietà distributiva. Nel terzo,quando si è moltiplicata la matrice Am per il vettore di potenze si ottiene:
Dunque si è dimostrato che:
Moltiplicando i due membri a sinistra per l'inversa di otteniamo:
che fornisce la nota variante ai famosi polinomi per il calcolo delle somme di potenze di interi successivi.
Esempio con m=11
Applicando il teorema:
O in forma equivalente:
Notare che questi polinomi differiscono da quelli stampati in Ars Conjectandi solo per il segno, in ogni polinomio, del coefficiente del monomio secondo per elevazione di grado.
7. Corollari
Abbiamo dimostrato che:
Vediamo ora alcune conseguenze dei due teoremi.
Per il teorema di Laplace sul calcolo delle matrici inverse si ha:
Le lettere minuscole con i relativi indici sono gli elementi delle corrispondenti matrici indicate da lettere maiuscole. Le matrici con doppio indice sono il complemento algebrico delle matrici di riferimento rispetto all’elemento indicato dagli indici di riga e colonna che sono invertiti per via della trasposizione nel processo di inversione di matrice.
In particolare:
7.1 Coefficienti di grado massimo
in questo caso il complemento algebrico è la matrice con indice immediatamente precedente e i determinanti di queste due matrici triangolari si ottengono moltiplicando gli elementi della diagonale principale.
7.2 Coefficienti dei monomi secondi per grado
Altrettanto immediato è il calcolo di:
anche in questo caso il complemento algebrico risulta una matrice triangolare per cui il calcolo è piuttosto semplice. Negli altri casi relativi alla stessa riga invece si avranno matrici non più triangolari per cui i calcoli risulteranno più complicati e, quindi, più difficili da generalizzare.
Viene quindi dimostrato e generalizzato quanto già osservato negli esempi mostrati.
7.3 Differenze tra la matrice G e la sua alternata
Abbiamo mostrato che
da cui si può ricavare:
che non solo conferma il valore opposto trovato negli esempi precedentemente mostrati ma dimostra che le due serie di polinomi per il calcolo delle somme di potenze di interi successivi differiscono solo per il monomio secondo per grado. dunque le due matrici corrispondenti differiscono solo di un valore per riga. La loro differenza è quindi una matrice di quasi tutti zeri così definibile:
7.4 Teorema sulla ripetizione di zeri nella matrice G e nella sua alternata.
Abbiamo visto precedentemente che salvo eccezioni esaminate i valori delle due matrici coincidono. Sappiamo inoltre che le matrici dei coefficienti dei polinomi per le somme di potenze di interi successivi, essendo inverse di matrici in relazione di alternanza (vedi 3.2) godono della stessa proprietà per cui per j+k dispari e non j=k+1 abbiamo:
quindi, in ogni colonna , salvo un’0eccezione, gli elementi con indice di riga più indice di colonna dispari dovranno essere uguali a zero
7.5 Numeri di Bernoulli
Per quanto visto precedentemente la prima colonna delle due matrici di coefficienti differiscono solo per il secondo elemento. Queste danno luogo a due varianti di sequenze quasi identiche che dal 1721, per iniziariva di Abraham de Moivre (1667-1754) sono conosciute come numeri di Bernoulli. In particolare si possono dare due definizioni :
Questa è la variante positiva (+½) considerata da Bernoulli nell’”Ars Conjectandi”
Questa è invece la variante negativa (-½) che oggi sembra essere più diffusa anche se molti autori le considerano entrambe.
7.6 I coefficienti dei monomi di primo grado
Calcolando come per gli altri coefficienti:
I complementi algebrici ritagliano le matrici eliminando prima riga e ultima colonna. Nel secondo caso si ottiene questa matrice:
Nel primo caso invece compare una matrice a segni alterni nelle posizioni con somma riga più colonna pari. Siccome di questa matrice interessa solo il determinante conviene considerare la sua alternata che non lo muta. La nuova matrice è a segni tutti negativi. Moltiplicando tutti gli elementi delle righe per -1 si ottiena la matrice Cm-1 ma il determinante risulta così moltiplicato per -1 m-1 volte. Dunque cambia segno quando m-1 è dispari.
7.7 Formula diretta per ricavare i numeri di Bernoulli dal triangolo di Tartaglia
Abbiamo dunque ricavato la seguente formula
Ecco degli esempi:
7.8 Formule ricorsive
Essendo queste matrici inverse
Il loro prodotto righe per colonne deve dare:
Queste formule per m=1 danno il valore di B0=1 per m>1 portano ad una formula che fornisce ricorsivamente Bn in funzione dei precedenti valori. Per esempio:
da cui si ricava:
o equivalentemente:
8. La formula rivelata in “ars conjectandi”
Nella pagina del libro di Jacob Bernoulli che abbiamo mostrato è data la seguente formula che qui esprimiamo in simboli attuali:
da cui si deduce facilmente anche
Notare che l’indice dei numeri di Bernoulli parte da due per cui è irrilevante specificare con il segno in apice a quale variante ci si riferisca.
Queste formule possono essere espresse anche in forma più compatta:
Ciò in forma compatta si può anche scrivere:
chi invece si ostina a voler privilegiare una delle due varianti dei numeri di Bernoulli dovrà complicare le cose usando una di queste:
naturalmente dato l’annullarsi dei numeri con indice dispari maggiori di 1 il fattore aggiunto serve solo a correggere il segno di ½.
Possiamo riassumere in forma didattica, come esempio relativo ai primi casi, quanto evidenziato dal libro di Bernoulli come segue:
Questo esempio fa intravedere la matrice Z6 caso particolare della matrice di c righe e c colonne definibile come:
Alla luce di tutto ciò possiamo dare una nuova definizione alle matrici già considerate:
Jakob Bernoulli non potè dimostrare il suo risultato. Noi invece, data l’unicità della matrice inversa, potremo farlo dimostrando che con le nuove definizioni risulta ancora:
Sapendo, come dimostrato,che i numeri di Bernoulli con indice dispari superiori a uno si annullano si vede facilmente che le due matrici sono una l’alternata dell’altra (vedi paragrafo 3). Per questo sarà sufficiente dimostrare solo una delle due uguaglianze, l’altra sara un’immediata conseguenza per quanto visto in 3.2. Procedendo per induzione si verifica facilmente il caso iniziale in cui c=1:
Si suppone poi la relazione vera per indice c-1:
Dobbiamo quindi dimostrare che:
Rispetto al caso precedente supposto vero, le nuove matrici da moltiplicare per ottenere la matrice unitaria, differiscono solo per l’ultima riga costituita da elementi diversi da zero e per l’ultima colonna composta di tutti zero salvo l’ultimo elemento. Dato che le c-1 righe della prima matrice acquistano uno 0 finale il prodotto con le varie colonne darà, con le prime c-1 colonne, i risultati precedenti cioè gli zeri e gli uno della matrice unitaria di ordine c-1.Quando le prime c-1 righe si moltiplicano per l’ultima colonna, essendoci uno zero per ogni addendo il risultato si annulla. Dunque nelle prime c-1 righe i valori trovati sono compatibili con l’elemento neutro del prodotto tra matrici. Rimane da mostrare che anche i valori dell’ultima riga sono zero salvo l’ultimo che è uno.
tenendo conto degli zeri della colonna j e di una identità binomiale
A questo punto si verifica facilmente che con j=c si ottiene B0 e quindi 1 mentre con j<c si ottiene una sommatoria nulla per quanto già dimostrato in 7.8
Essendo dunque la matrice prodotto uguale all’elemento neutro abbiamo dimostrato che i coefficienti per la somma delle potenze di interi successivi possono essere espressi in funzione dei numeri di Bernoulli come indicato in “Ars conjectandi”.
9.L’algoritmo di Ada
Nel 1842 il matematico ingegnere Charles Babbage (1791-1881) tenne un seminario presso l’università di Torino, e Luigi Menabrea, giovane ingegnere italiano, pubblicò un libro in francese sul progetto[4]. Baggage incaricò Ada Lovelace nata Byron, figlia del noto poeta romantico che alla sua nascita l’aveva abbandonata insieme alla madre. Ada, allevata dalla madre che l’aveva avviata allo studio dei numeri era diventata una stimata matematica e collaborava con l’ideatore della macchina analitica che ne lodava le capacità appellandola “incantatrice di numeri”. Il saggio fu quindi tradotto e arricchito dalle note di Ada che alla fine portarono le pagine complessive da venti a cinquanta.
Nota G di Ada Lovelace. Algoritmo per il calcolo dei numeri di Bernoulli in un programma pensato per la macchina analitica di Charles Babbage, un primo computer basato sulla meccanica che per i suoi alti costi non fu mai realizzato. |
Nella nota G. si può vedere, come era in “Ars conjectandi”, che non vengono considerati tutti quelli che oggi si considerano numeri di Bernoulli. Non si considerano B0 e B1 ma si comincia dal successivo per cui gli indici usati nel programma, visibili sul lato destro, B1 B3 B5… corrispondono ai nostri B2 B4 B6... L’algoritmo usato evita il calcolo dei valori nulli. Utilizzando la nostra notazione può esprimersi come:
Tenendo conto che nell’ultimo termine della somma si ha
si può isolare l’ultimo addendo ottenendo:
da utilizzare per n>1. Per n=1 invece abbiamo semplicemente
La formula nonostante le apparenze coincide con quella che abbiamo già dimostrato in 7.8:
Infatti risulta
e anche:
Se si parte dalla forma esplicita vera per m>0
si ottiene
da cui facilmente si arriva alla più generale
che calcola anche i valori nulli corrispondenti agli indici dispari per m>2
10. La via analitica
Finora ho seguito la via matriciale, una via elementare che mi sono aperto senza poter sapere se qualcuno mi abbia o meno preceduto. Attraverso questa via è stato possibile dimostrare alcune proprietà di questi numeri. Attualmente invece mi pare si percorra soprattutto la via analitica, aperta dalla analisi matematica. Qui i numeri bernoulliani non sono definiti in relazione al problema che storicamente ce li ha fatti conoscere ma attraverso concetti più complessi e problematici come le serie infinite. Ora mi propongo sia di presentare questa questa via più frequentata sia di collegarla alla mia via.
10.1 Funzione generatrice, varianti negativa
Nella nota G scritta da Ada [3] viene presentata la formula che abbiamo visto e questa viene giustificata spiegando in che modo si possa ricavare da un particolare sviluppo in serie dove appaiono gli stessi numeri già incontrati da Bernoulli. E’ questa la cosiddetta funzione generatrice per i numeri di Bernoulli nella variante con B1 negativo:
L’uguaglianza è ristretta al caso x<2 (raggio di convergenza della serie)
(raggio di convergenza della serie)
Questa uguaglianza è un notevole risultato dell’analisi matematica. E’ lo sviluppo in serie di Maclaurin. Per questo sviluppo si devono calcolare i valori della funzione e delle derivate successive nel punto x=0 dove tutte queste funzione non sono definite e quindi si devono calcolare i limiti per arrivare a determinare in questo modo i numeri di Bernoulli.
Ma cosa assicura che in questo modo lungo e laborioso usciranno sempre e solo gli stessi numeri incontrati da Bernoulli affrontando tutt’altro problema?
Per dimostrare questa identità seguirò la strada indicata anche da Ada nelle sue note.
Si considera il notissimo sviluppo in serie di Maclaurin della funzione esponenziale:
e si sostituisce nella funzione generatrice ottenendo:
Quindi considerando lo sviluppo in serie:
da cui
e moltiplicando i polinomi infiniti:
Notare che i monomi dello stesso grado si trovano sulla diagonale. Con la messa in evidenza delle potenze crescenti si ha:
Utilizzando i coefficienti binomiali e ricordando:
possiamo scrivere:
Ora è evidente che perché questa uguaglianza sia possibile non solo deve essere B0=1 ma si devono annullare anche tutti i coefficienti degli infiniti monomi. Dunque per ogni intero m>1 deve essere:
che è la legge che abbiamo già incontrato e che ci garantisce che anche con lo sviluppo in serie si ha lo stessa sequenza numerica bernoulliana.
Anche se abbiamo preferito non appesantire la notazione specificando qui si intendono i numeri di Bernoulli nella variante negativa.
10.2 Funzione generatrice, variante positiva
Sommando x ai due membri della prima uguaglianza otteniamo la seconda, funzione generatrice della variante positiva B1=1/2 dei numeri di Bernoulli
infatti al primo membro si ha:
mentre al secondo sommando gli unici due monomi di primo grado si ha il cambio di segno di B1.
Si può notare che la seconda funzione generatrice si ottiene dalla prima anche sostituendo x con il suo opposto. Ciò però dovrebbe cambiare segno a tutti i monomi di grado dispari ma ciò invece non risulta. Come è possibile? E’ possibile in quanto abbiamo già dimostrato, e ora è confermato, che tutti i numeri con indice dispari superiore ad uno valgono zero e dunque il cambio di segno non ne muta il valore.
11. Altre relazioni con le matrici considerate
Mostriamo qui argomenti, anche non completamente sviluppati, che lasciano intravedere l’utilità dell’approccio matriciale utilizzato in questo saggio.
11.1 Relazione di Am con i polinomi di Bernoulli
Riprendiamo in considerazione Am così definita:
se invece di moltiplicare la matrice inversa per il vettore di potenze di n, come già visto, moltiplichiamo per il vettore delle sue derivate prime otteniamo:
Dove Bi(n) è l’ i-esimo polinomio di Bernoulli
Esempio per m=11:
Notare che questi polinomi sono le derivate prime di quelli per le somme di potenze di interi successivi. La relazione tra le matrici è la seguente:
dove Mnè la matrice dei coefficienti dei polinomi di Bernoulli Nn è una matrice con tutti elementi nulli tranne la diagonale principale dove compaiono in sequenza i numeri naturali. La sua inversa invece ha i reciproci in diagonale.
Esempio:
O anche per quanto dimostrato in 8 :
dove:
Da quanto precede si può anche osservare che risulta anche
Per quanto riguarda la matrice inversa si ricava facilmente:
che quindi si ricava facilmente dalla An dividendo tutti gli elementi delle varie righe per gli interi successivi. Si ricava quindi facilmente (come fatto in 7.5) anche:
dove A’n è una matrice di n righe e n colonne facilmente ricavabile dal triangolo di Tartaglia che può essere definita come segue:
esempio:
Da notare che se si moltiplicano le righe per il reciproco del loro primo elemento il determinante viene moltiplicato per 7! per cui si ritorna alla precedente formula:
.
11.2 Fattoriali crescenti, decrescenti e numeri di Stirling
Si chiamano fattoriali crescenti di x i seguenti prodotti
e così via |
Si chiamano fattoriali decrescenti di x i seguenti prodotti
|
I coefficienti dei polinomi espansi sono i numeri di Stirling di prima specie e, i primi casi esaminati, possono anche essere espressi come:
Sappiamo che le due matrici alternate avranno inverse alternate. Queste corrispondono ai numeri di Stirling di seconda specie:
che nella forma positiva corrispondono anche al numero di partizioni di un insieme in un certo numero di classi.
Risulta:
e anche:
11.3 Altre relazioni notevoli
Per ogni intero positivo n vale anche:
12. Bibliografia
Cong Lin On Bernoulli numbers and his properties 2004 (Ptagora Archimede.. Al K.)
[1] Jacobi, Carl Gustav Jacob (1834). "De usu legitimo formulae summatoriae Maclaurinianae". Journal für die reine und angewandte Mathematik. 12. pp. 263–72
[3] Mcmillan, Sondow Proof of power sum and binomial coefficient congruences via Pascal’s identity digitalizzato su Internet archive, 2010
[4] Luigi Federico.Manebrea, Notions sur la machine analytique de Charles Babbage, 1842, Bibliothèque Universelle di Ginevra