|
4. Due osservazioni geometriche |
|
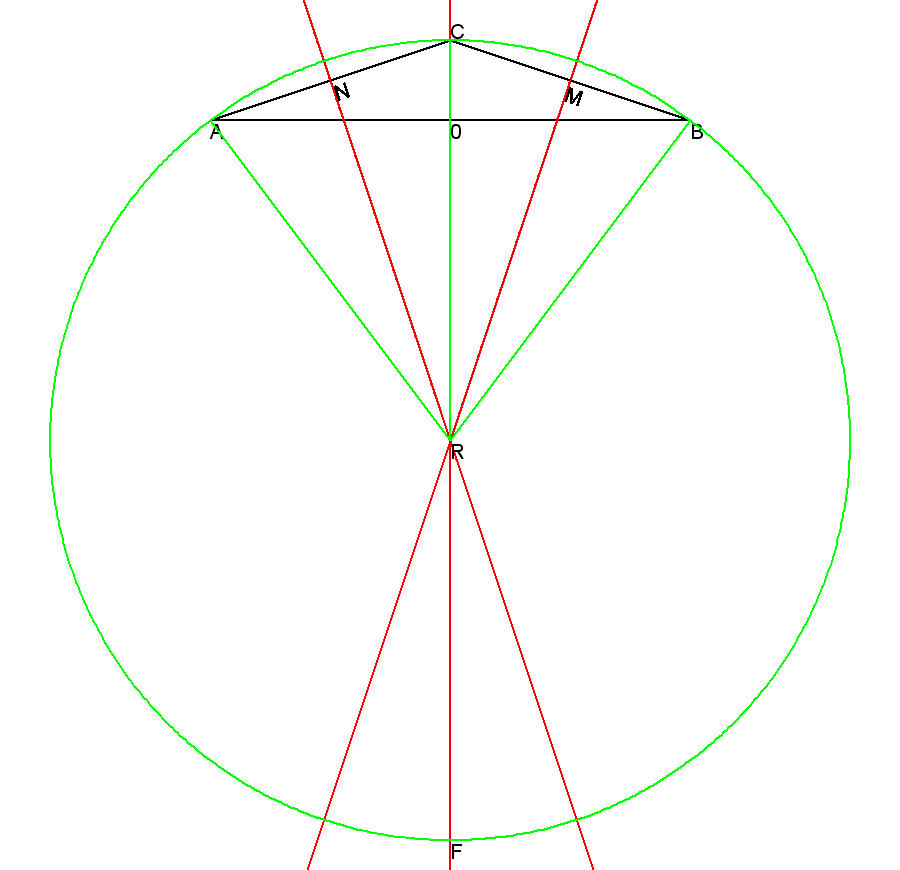
Osservazione 1 - Abbiamo ottenuto 4 triangoli rettangoli uguali: ARN=NRC=CRM=MRB Dunque l'angolo ARB=4*CRM |
| Osservazione 2 - Il triangolo rettangolo CMR è simile a COB. Infatti oltre all'angolo retto hanno l'angolo RCB in comune e dunque, necessariamente, essendo la somma degli angoli interni uguale ad un angolo piatto, anche il terzo angolo deve essere uguale, per cui CBO=CRM. Dunque per similitudine si ha: CB/CO=CR/CM |
|
Nota, facoltativa. Questa nota, semplice corollario dell' osservazione 2, può essere omessa senza pregiudicare la comprensione del problema. Essendo CM=CB/2, sostituendo si ottiene CB/CO=2CR/CB da cui facilmente CB*CB=2CR*CO Così abbiamo anche dimostrato, a nostra insaputa, niente meno che il primo teorema di Euclide! (Cliccare per vedere di più) |
 |