Verso un pentagono plastico 2/2 

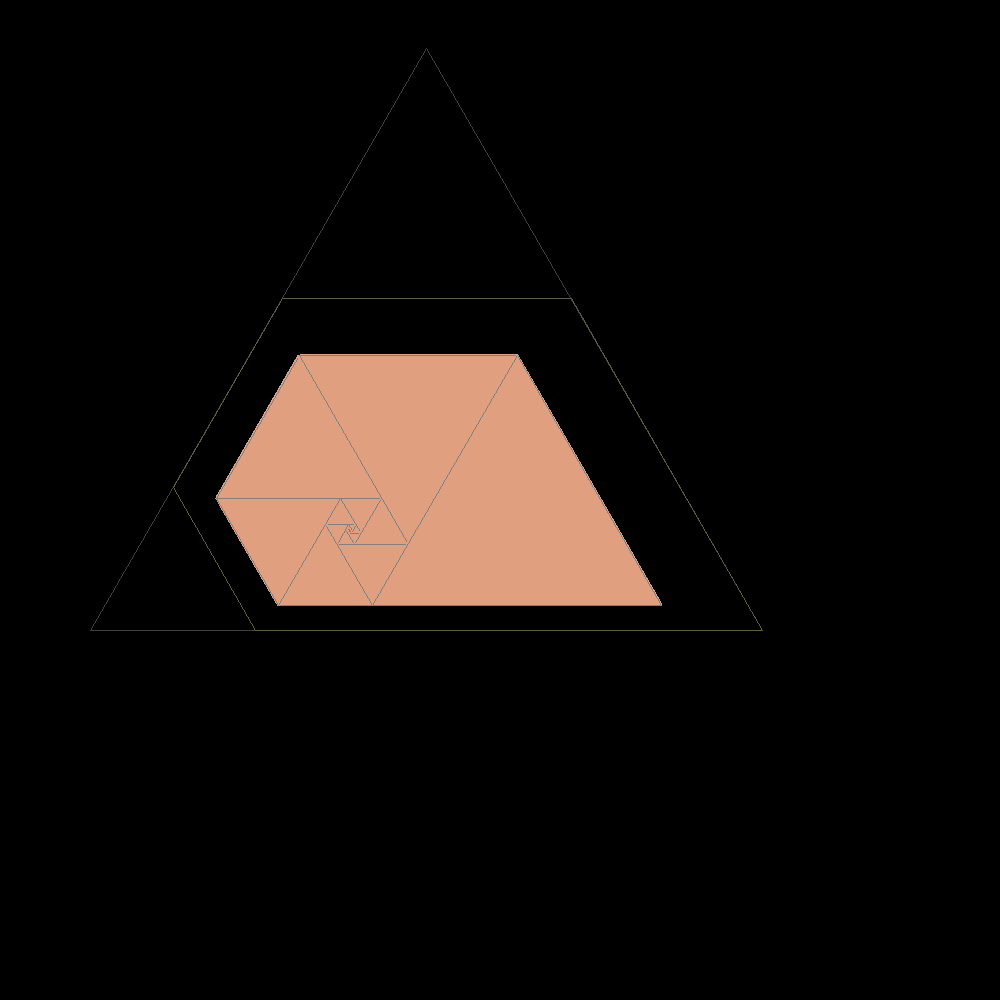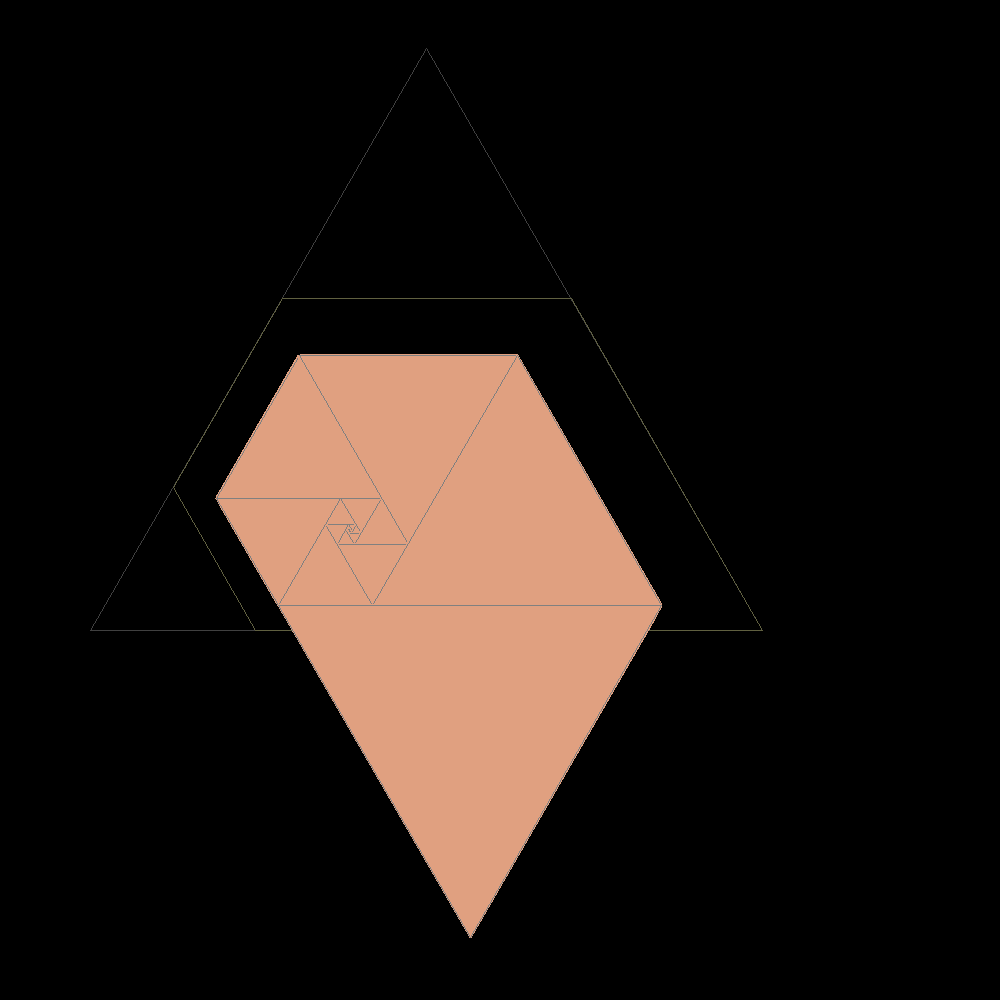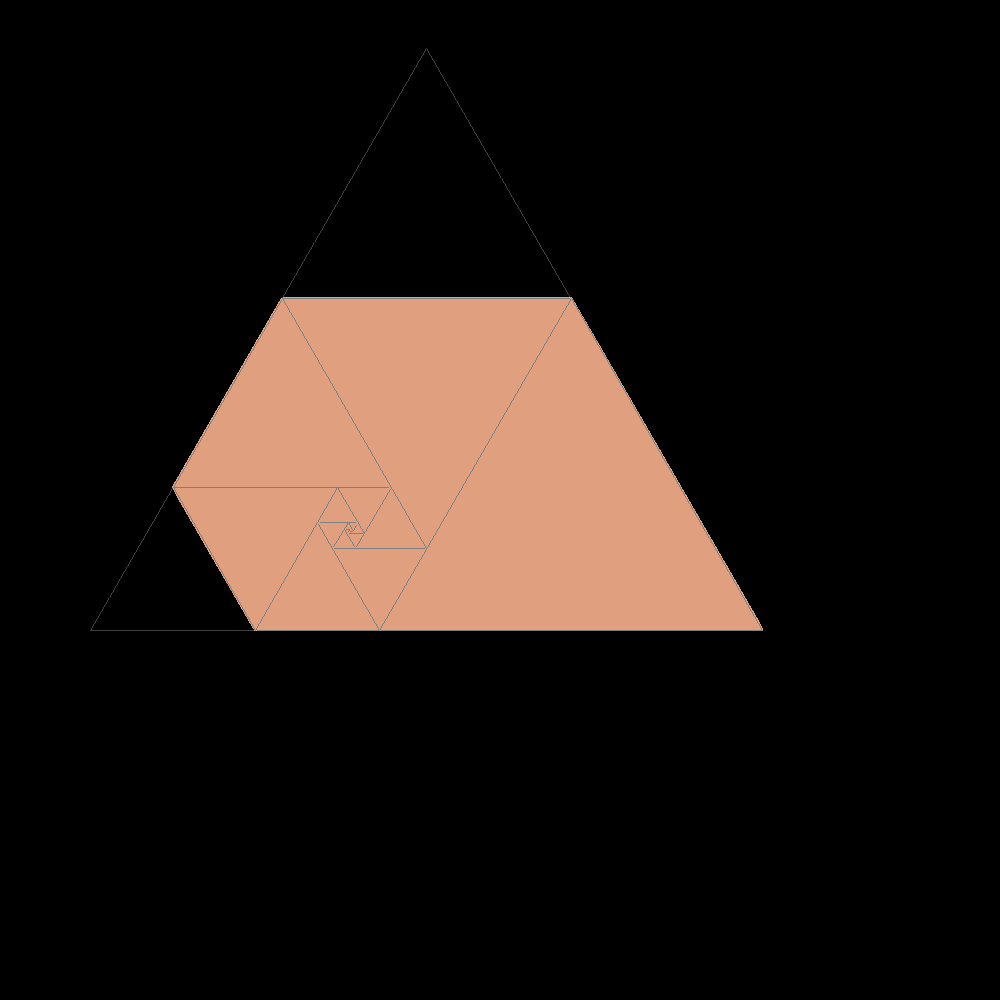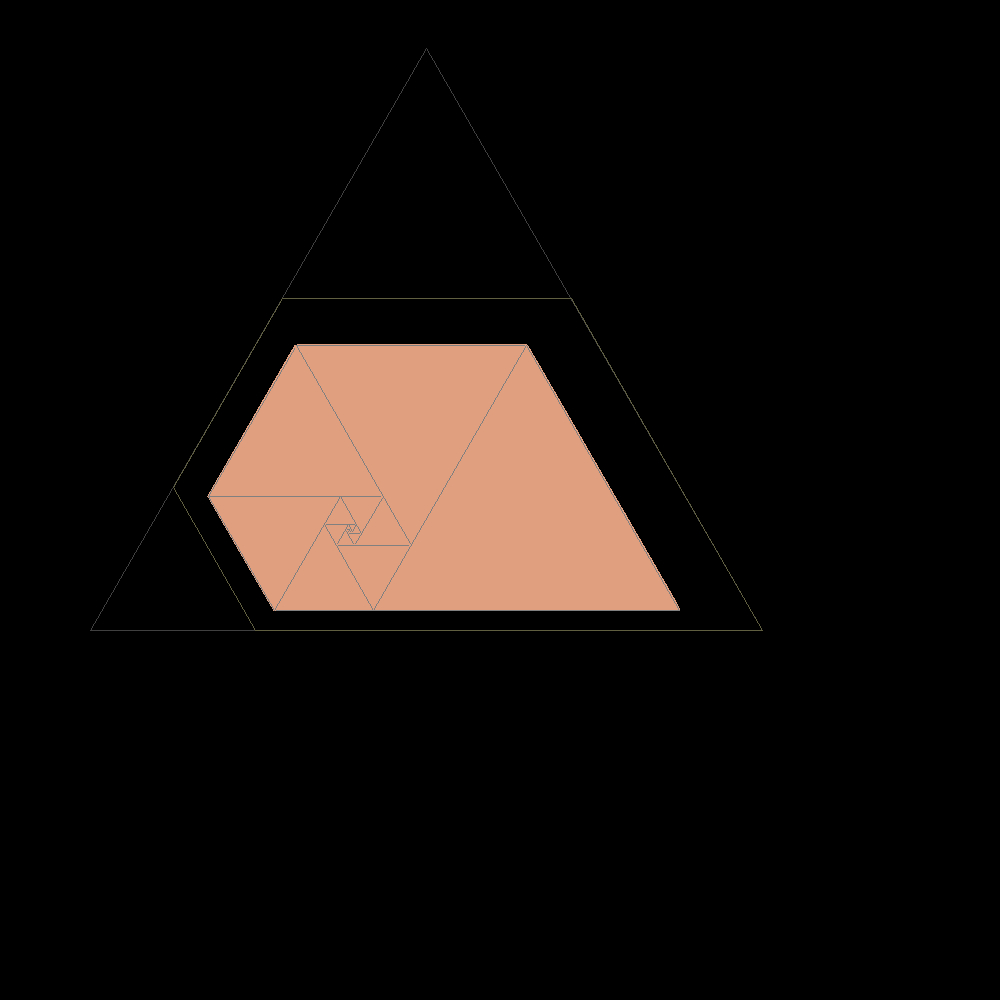
Dal rettangolo  ottenuto si osserva che il lato di un quadrato uguaglia la somma tra il secondo e il terzo dopo di lui in ordine decrescente. Per  questo si può tendere al rettangolo plastico costruendo rettangoli di quadrati secondo questa sequenza :

1, 1, 1, 2, 2, 3, 4, 6, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265, 351, 465, 616, 816, 1081,...

che sono proprio i famosi numeri plastici di Padovan analoghi a quelli di Fibonacci. Anche con questi si potrebbero contare le coppie di conigli nell'ipotesi aggiuntiva che siano mortali.
Il rapporto tra due numeri consecutivi della successione tende la rapporto tra lato minore e il maggiore del rettangolo plastico

0.7548776662...=1/P (numero plastico P=1.324717957...)
soluzione dell'equazione:
r³+r²-1=0    (numero aureo f=1.6180339887499...)

English version
Plastic rectangle and Padovan sequence