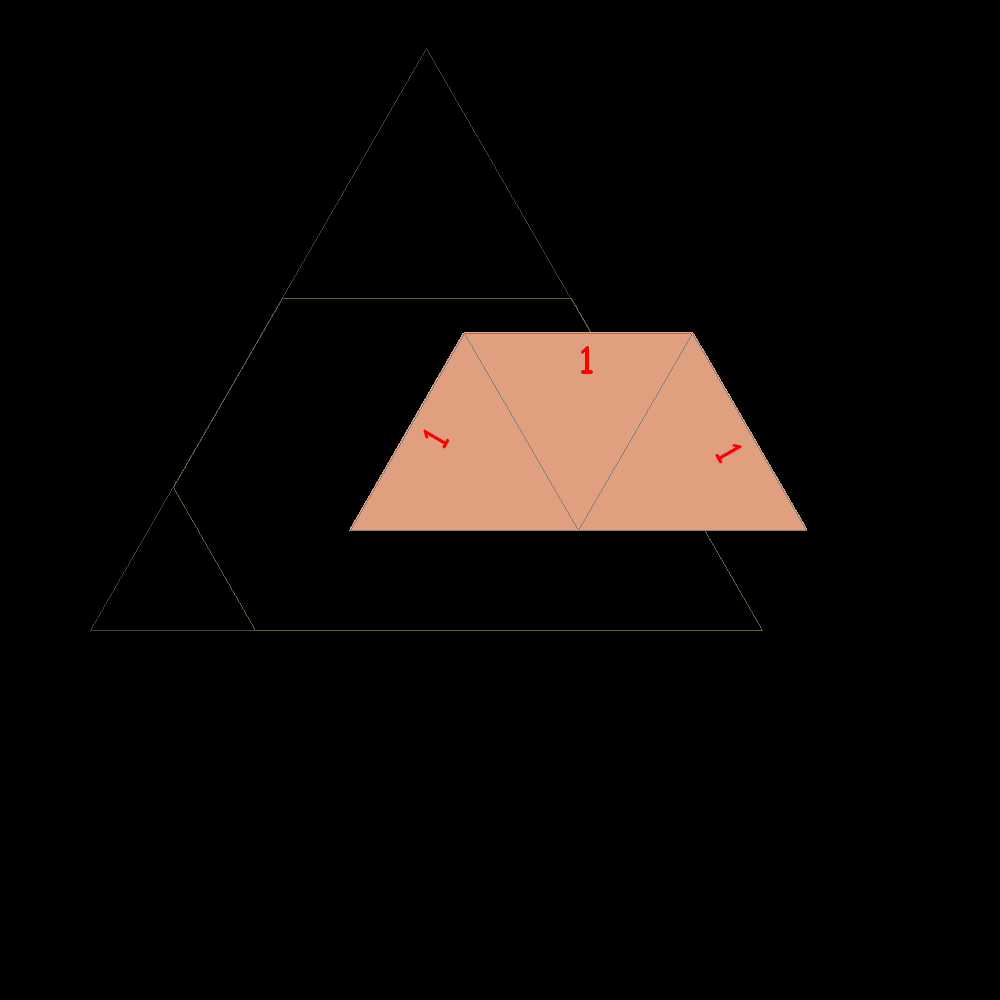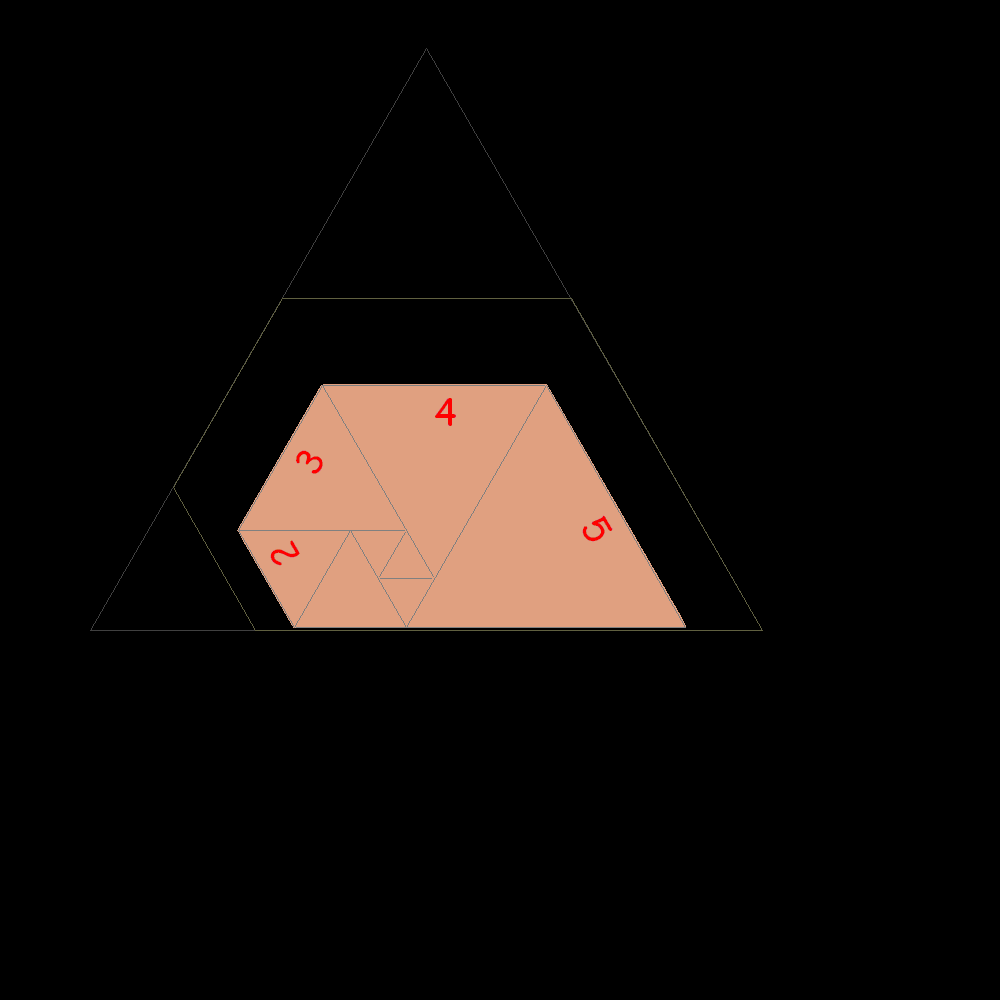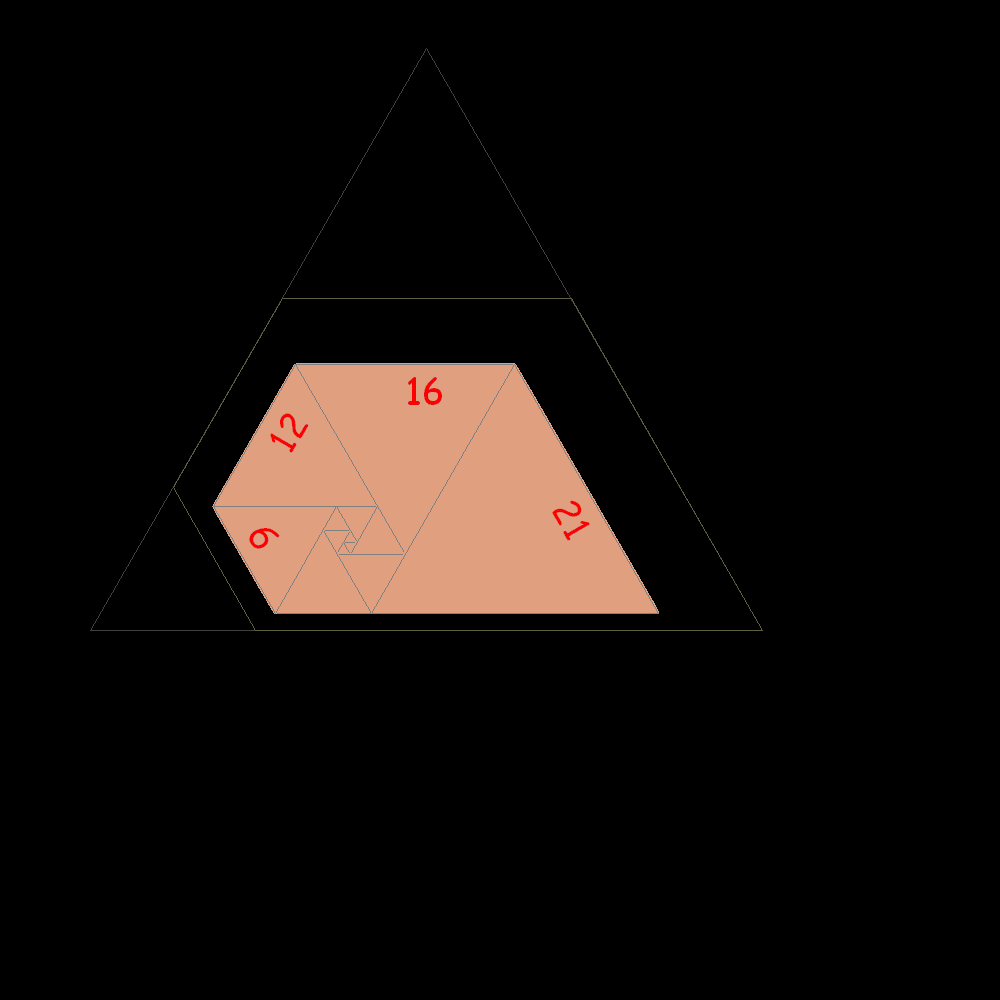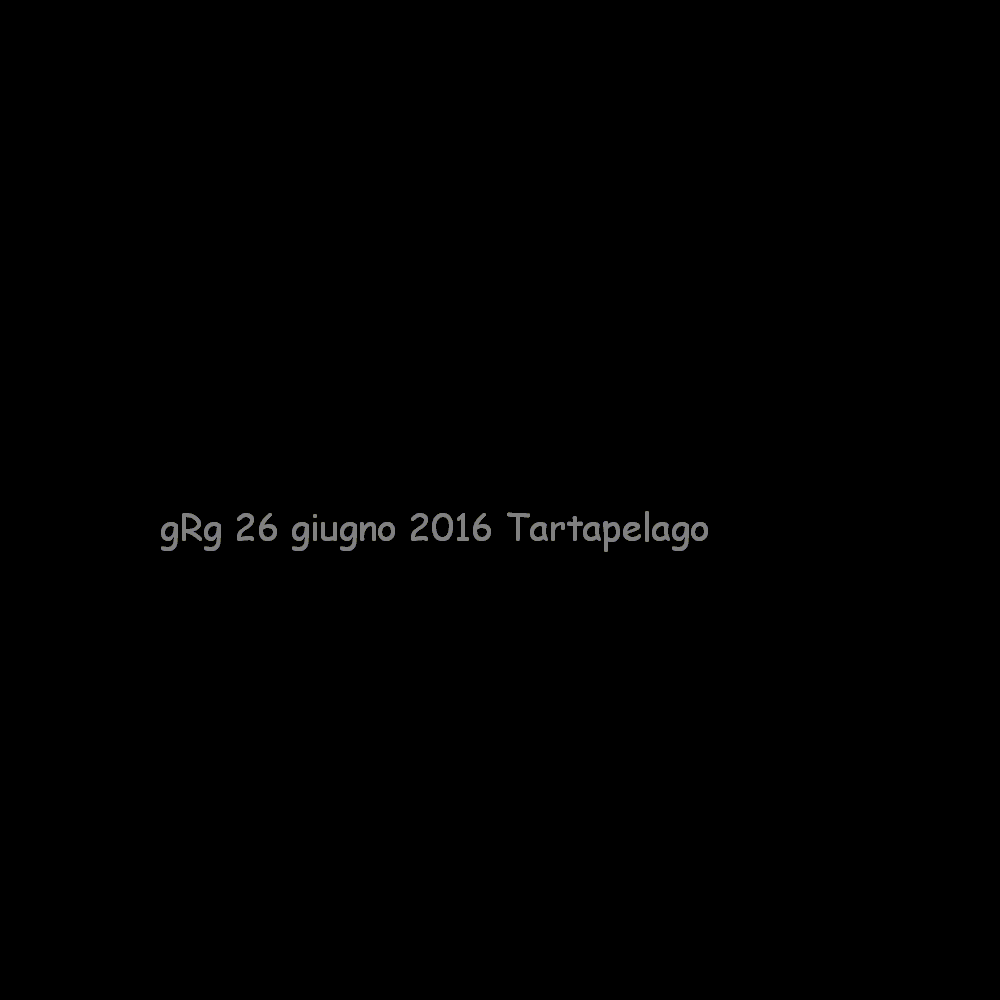
Verso un pentagono plastico 1/2 

Dalla sequenza si osserva che il lato di un nuovo quadrato uguaglia la somma tra il secondo e il terzo prima di lui.

1, 1, 1, 2, 2, 3, 4, 6, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265, 351, 465, 616, 816, 1081,...

Questi sono  i  numeri plastici di Padovan analoghi a quelli di Fibonacci. Anche con questi si potrebbero contare le coppie di conigli nell'ipotesi aggiuntiva che siano mortali.
Il rapporto tra due numeri consecutivi della successione tende la rapporto tra lato minore e il maggiore del rettangolo plastico

0.7548776662...=1/P (numero plastico P=1.324717957...)
soluzione dell'equazione:
r³+r²-1=0    (numero aureo f=1.6180339887499...)

English version
Plastic rectangle and Padovan sequence